这篇是继 深度学习在序列化推荐中的应用 和 深度学习在序列化推荐中的应用(2) 的补充理解
base idea:设计了一个local activation unit来学习用户行为历史的兴趣点
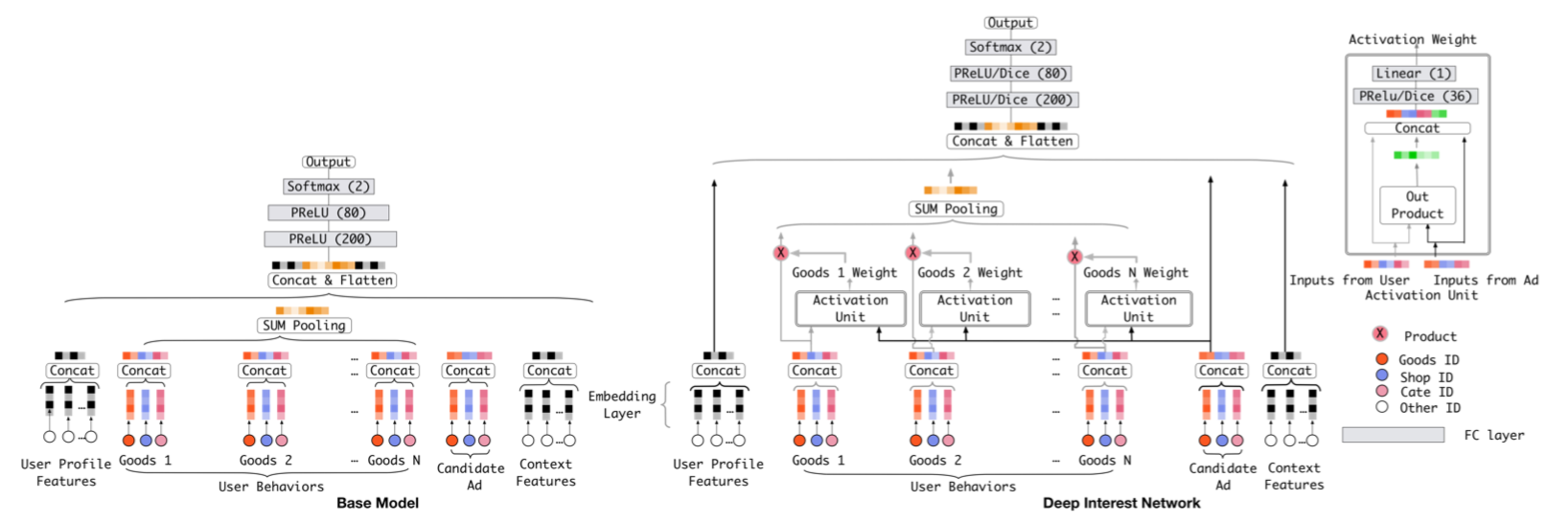
一般传统的深度模型是将各类的用户信息（包括用户行为）查询到Embeddings之后通过各种MLP层来灌入到最后隐层，而上图（右）的DIN模型中 根据当前Item的信息与 用户的行为历史进行交互获取其历史中的兴趣，其核心就是local activation unit：
协同过滤(Collaborative Filtering,简称CF)是Amazon在2001年提出的应用于推荐领域的一个算法，至今各大家的推荐系统中都能见到协同过滤的影子，是推荐领域最经典的算法之一
在实际场景中可以将用户对于Item的评分/购买/点击等行为 形成一张user-item的矩阵，单个的User或者Item可以通过对于有交互的Item和User来表示(最简单的就是One-Hot向量)，通过各种相似度算法可以计算到User2User、Item2Item以及User2Item的最近邻，先就假设按User2Item来说:
本文主要是对于An overview of gradient descent optimization algorithms的学习和理解，方便记忆
梯度下降法是非常著名的优化算法之一，思想简单高效，被各种深度框架(Tensorflow、Pytorch)用做默认优化器。
梯度下降法是最小化目标函数的一种方法，利用目标函数梯度的反方向更新参数，沿着目标函数的斜面下降的方向，直到到达谷底。
由于被广泛使用，因此在梯度下降法出了很多变种以及许多优化算法，并且他们同时都是朝着加速收敛的方向进行优化。
基于上一篇GRU4REC的继续聊聊深度学习在推荐系统中的应用
作者提出了一种混合Encoder的方式：全局(Global)所有的序列信息的Encoder和当前(Local)Session序列的Encoder
所以他的模型是：
用户在互联网应用上的绝大部分的行为都是可以用一个序列来表示，比如购物、听音乐、看feed流等，用式子来表示就是$${x_1,x_2,x_3,..,x_N} -> x_{N+1}$$
因此对于这个序列如何建模来获取整个用户的意图行为至关重要，而之前传统的ML只能基于统计或者经验的方式来尽量抽取这些序列信息，并无法hold整个序列，16年提出的GRU4REC利用RNN-Based对用户序列进行建模并且取得了不错的效果，同时也会有一些研究对于GRU4REC做了不少改进和扩展，本文主要对GRU4REC以及扩展做一些简答的自我了解和记录。
也是一篇在CTR预估中堆Deep层数的轮子文，先来了解一下：
FM的特征组合能力灌给DNN进行joint-train不过xDeepFM所提出的点是结合RNN和CNN的特性完成多阶特征的抽取，并且最终和和DNN以及Linear整合到一起完成显性特征的使用。
CTR预估一直以来都是工业界搜索、广告和推荐中的核心，而传统的LR模型（逻辑回归）几乎可以被称为CTR界的神算法，虽然他结构非常简单，但是他计算速度特别快，并且在加以特征工程师的修饰，一样可以拿到很好的效果。
但是这样的操作毕竟特征的选择会起比较重要的作用，如果遇到不同任务需要重新提取不同类型的特征。在2014年Facebook通过GBDT的生成LR特征的方式，取得了不错的效果。众所周知，GBDT中的策略树将会有一定的特征选择功能，因此该方式先原先（未经过太多特征工程的特征过一把GBDT），将GBDT的叶子节点作为特征继续输入到LR模型中，最终对目标的CTR值进行预测。
除特征工程外，LR的另一个缺陷就是对于高阶的表达能力不足，从这两个出发点，结合公司中手头的一些工作，整了下最近比较经典的Paper来说说深度学习在CTR预估中的一些方法，主要有:FNN、PNN、Wide&Deep、Deep&Cross、DeepFm、NFM.
近期使用
FM系列完成了一个CTR预估的任务，本文是阅读了一些paper之后对于FM、FFM、DeepFM、NFM,AFM的一个理解和记录
Factorization Machine(FM)由Steffen Rendle在2010年提出，旨在解决系数数据下的特征组合的问题，目前该系列模型在搜索推荐领域被广泛使用。
先来看一个经典的电影评分问题
隐马儿可夫模型（hidden Markov model,HMM）是描述隐藏的马尔科夫链随机生成观测序列问题，属于生成模型。
HMM描述了一个隐藏马尔科夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生的观测随机序列的过程：
状态序列观测序列