By

文章目录
  1. 1. 题目
  2. 2. 解析
  3. 3. 代码
  4. 4. 参考

题目

输入一个字符串,输出该字符串中对称的子字符串的最大长度。比如输入字符串 “google”,由于该字符串里最长的对称子字符串是“goog”,因此输出 4。

解析

该题目比较直观的解法有：

  1. 暴力法：遍历所有可能的子串，然后判断子串是否为回文，故总得复杂度为O(n^3)
  2. 遍历字符串，以当前遍历为中心点，然后向两边扩展，直至扩展到不是回文，总复杂度为O(n^2)

还有后缀树也可以解，不过需要较大的空间，本文使用的是manacher算法：

Manacher最早发现了可以用O(n)的时间复杂度来解决该问题，所以这种方法称之为Manacher算法。

现在以查询字符串”abaab”为例，该算法为了将”aba”和”baab” 奇偶形式统一考虑，做了一个很精妙的预处理：每每两个字符串以及两端都加一个标志符号#，就形成了
“#a#b#a#a#b#”新字符串，那么”aba”则可以看做”#a#b#a#”，同时”baab”转为#b#a#a#b#”，就都为奇数形式了

假设当前的字符串长度为n,则添加的#个数为2*n+1

接下来需要添加一个辅助数组p,其中p[i]的值表示第i位上可以形成的最大回文半径(比如p[1]=2 因为#a#的半径为2)，全部先列出的话为：

新串:# a # b # a # a # b #
p[]:1 2 1 4 1 2 5 2 1 2 1

其实我们可以通过p[i]的值就可以得到每个字串相应位置的回文长度

半径p[i]的回文长度为2*p[i]-1，而每个在新字符串上每个回文两端必定是#，也是也就是相当于对原回文做了#的添加操作，假设原回文串为x长度，根据上面的添加#计算方式得到添加后的回文串为2*x+1
故2*p[i]-1=2*x+1 
可得x=p[i]-1

那么现在的问题就是相当于如何求出新字符串上p数组各个元素的值了,当然计算这个也不能靠暴力来算，不然就没意思了，大概我们了解到计算p[i]的时候 p[j]的值都是已经算出来了，同时回文串有对称性质，所以我们接下来可以这么看

现在要求p[5]，根据P[3]=4可知，p[5]是包含在p[3]的回文串中，又因为回文的对称性，所以p[3]左侧一定存在一个字符串与p[5]一致，
其实这里就可以算出其对称串为2*3-5=1  也就是p[1]，P[1]是已经算出的=2  所以p[5]也必定至少为2（这里要考虑P[3]回文的右界，不能超过）
所以此时p[5]只需要从p[3]和p[7]往两侧扩展即可，判断其存在的最大回文，这样就可以大大减少了重复计算

接下来借用别人的图来解释一下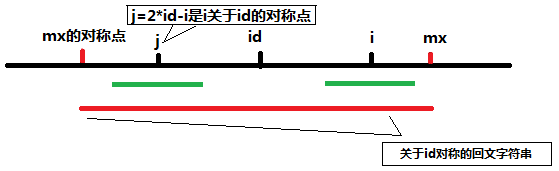

对应上面的例子你可以将变量这么认为:i=5,id=3,j=1(通过2*id-i计算) 而mx=p[id]+4，其中id表示先前存在的能到最大右边的回文中心标记。。。

所以当mx>i的时候 就可以说明在计算i的时候 可以根据id找到左侧对应的点 这样就可以减少计算量

但是另一种情况就是p[j]的回文范围超越了p[id]的回文范围，那这样就不能完全使用p[j]的值了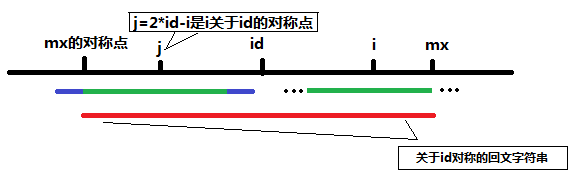

此时p[i]已知的最大可确保回文的范围就是mx-i

综合上述：初始化p[i]=min(p[2*id-i],mx-i) 当mx>i

好，该算法的核心已经说明了接下来直接上代码：

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
/**
 * Manacher 方法
 * 通过增加#字符将问题统一转为奇数回文的计算
 * 借助半径辅助数组，每次计算当前辅助数组的值的时候
 * 利用回文的对称性可能避免重复计算
 * @param str
 * @return
 */
public static String manacher(String str)
{
	int len=(str.length()<<1)+1;
	char[] f=new char[len];//将每每两个字符中间加上#，同时首位也加#
	int[] p=new int[len];//辅助数组 存储对应索引上能形成最大回文的半径
	
	
	for(int i=0;i<str.length();i++)
	{
		f[i<<1]='#';
		f[(i<<1)+1]=str.charAt(i);
	}
	f[len-1]='#';
	
	int id=0,maxId=0,maxLen=0,maxIndex=0;
	for(int i=0;i<len;i++)
	{
		if(maxId>i)
		{
			p[i]=Math.min(p[2*id-i], maxId-i);//找到对称点
		}else{
			p[i]=1;
		}
		
		//继续往两边进行回文判断
		while((i-p[i])>=0 && (i+p[i])<len && f[i+p[i]]==f[i-p[i]])
			p[i]++;
		
		//更新当前可以到达的最远的索引id
		if(p[i]+i>maxId)
		{
			maxId=p[i]+i;
			id=i;
		}
		
		//更新最大半径以及索引位置
		if(p[i]>maxLen)
		{
			maxLen=p[i];
			maxIndex=i;
		}
	}
	
	//构造回文字符串
	char[] ret=new char[maxLen-1];
	int j=0;
	for(int i=maxIndex-maxLen+1;i<maxIndex+maxLen;i++)
	{
		if(f[i]!='#')
			ret[j++]=f[i];
	}
		
	return String.valueOf(ret);
	
	
}

测试的一些样例为

1
2
3
4
5
6
7
public static void main(String[] args)
{
	System.out.println(manacher("abaab"));
	System.out.println(manacher("google"));
	System.out.println(manacher("adfdfsedasdxdsa"));
	
}

结果：

baab
goog
asdxdsa

他们都说这个方法复杂度为O(n)，应该也是，主要是比较maxId，其余的重复已经都是可以根据前面的结果算得

参考

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权

文章目录
  1. 1. 题目
  2. 2. 解析
  3. 3. 代码
  4. 4. 参考