求最小编辑距离

文章目录

问题链接：https://leetcode-cn.com/problems/edit-distance

给定两个单词 word1 和 word2，计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

输入: word1 = "horse", word2 = "ros"
输出: 3
解释: 
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

则需要维护一个二维的最小编辑距离表：

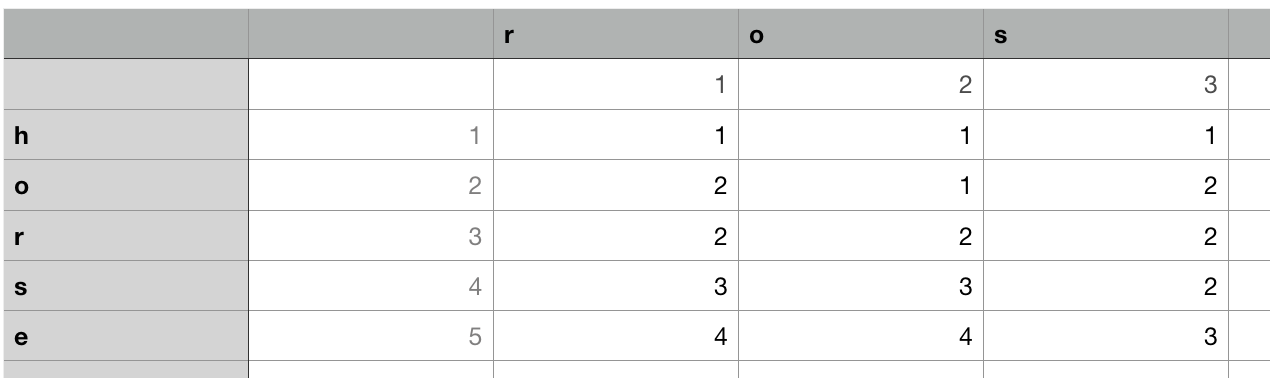
则右下角则为最小的编辑距离，核心代码为:

int minDistance(string word1, string word2) {
        int M = word1.length();
        int N = word2.length();
        int A[M+1][N+1];

        for(int i=0;i<=M;++i){
            for(int j=0;j<=N;++j){
                if(i==0){
                    A[i][j] = j;
                }else if(j==0){
                    A[i][j] = i;
                }else{
                    A[i][j] = 0;
                }
            }
        }


        for(int i=1;i<=M;++i){
            for(int j=1;j<=N;++j){
                if(word1[i-1] == word2[j-1]){
                    A[i][j] = A[i-1][j-1];
                }else{
                    A[i][j] = min(A[i-1][j-1],min(A[i-1][j],A[i][j-1]))+1;
                }
            }
        }

        return A[M][N];
    }