RankSvm-基于点击数据的搜索排序算法
RankSvm是Pairwise的学习排序中最早也是非常著名的一种算法,主要解决了传统PontWise构建训练样本难的问题,
并且基于Pair的构建的训练样本也更为接近排序概念
基本介绍
RankSvm是在2002年提出的,之前工作关于LTR的工作貌似只有Pointwise相关的,比如PRanking,这样的排序学习算法Work需要含有档位标注的训练样本,一般有以下几种获取方式:
- 需要人工/专家标注
- 诱导用户对展现的搜索结果进行反馈
而RankSvm只需要根据搜索引擎的点击日志构建Pair对即可,相对于先前的工作在算法的实用性上有了非常大的改善。
训练样本设计
一般搜索引擎都会记录用户搜索后展现的结果以及用户的点击情况,这种日志成本较低,并且改造系统也较为方便,而RankSvm的训练样本就是从这种点击日志中进行提取。
由于用户点击的doc概率和排序的位置影响很大,虽然一般都是偏爱相关性较大的doc,但是如果这种doc排在很后面的话其实用户也几乎不会点,所有rankSvm就只考虑top级别的点击日志,一般为top 10
另外在构建训练数据时同一query下认为用户被点击doc相关性要高于没有被点击的doc,但是由于用户是从上往下浏览网页的,所以排在前面的doc被点击的概率会大于后面的doc,因此RankSvm使用的最终策略为:
pair构建策略:给定一组排序情况($doc_1,doc_2,doc_3,…$),以及$C$记录了用户点击doc的情况,则有
$$doc_i{\overset{r^*}{<}} doc_j$$对于所有pair对$1 \leq i$,同时$i \in C$ ,$j \notin C$
$r^*$表示应有的优化排序,也就是被点击文档的相关性要大于排在该文档前面并且未被点击的文档,看上去很绕口,看个栗子:
假如某个用户搜索某个query得到首页10个doc,按顺序使用$doc_i$进行表示,如果该用户点击了$1,3,7$三个文档,则认为有:
$$doc_3 {\overset{r^*}{<}} doc_2 \\
doc_7 {\overset{r^*}{<}} doc_2 \\
doc_7 {\overset{r^*}{<}} doc_4 \\
doc_7 {\overset{r^*}{<}} doc_5 \\
doc_7 {\overset{r^*}{<}} doc_6$$
表示该query下$doc_3$的相关性要高于$doc_2$,理应排在前面,而$doc7$的相关性也应该要高于$doc_{2,4,5,6}$,但是可以发现未见$doc_1$的相关性鉴定,这是由于$doc_1$已经是排在了第一位,本身位置点击概率就就是最高的,所以无法判断与其他文档相关性的高低,同理,$doc_{8,9,10}$也未纳入相关性的排序中。
训练样本可以通过这样方式进行构建,但是遗憾的是并没有一种机器学习算法能直接使用这种数据进行训练学习-_-
基本思想
在上面的栗子中,我们希望用新算法完成$doc_{1,3,7}$排在top 3,那这样的文档的真实相关性高的将会排到前面,RankSvm采用$Kendall’s \quad \tau$来统计实际排序与算法排序的度量,先看下面两个变量:
- $P$表示排序序列中保持一致性的
Pair对数量,也就是真实相关性高的排在第的前面。 - $Q$表示排序序列中保持不一致的
Pair对数量(就是为逆序了),也就是由于算法的误差导致真实相关性低的排在了高的前面 - 同时$P+Q=\binom{m}{2}$,$m$表示序列中文档的数量,因为长度为$m$的序列可能组成的
pair对为$m$的2组合
则$\tau$的计算方式为:
$$\tau(r_a,r_b)=\frac{P-Q}{P+Q}=1-\frac{2Q}{\binom{m}{2}}$$
$r_a$为真实排序,$r_b$为算法排序
比如实际文档中的顺序为:
$$d_1{\overset{r^*}{<}}d_2{\overset{r^*}{<}}d_3{\overset{r^*}{<}}d_4{\overset{r^*}{<}}d_5$$
但是算法的排序顺序为:
$$d_3{\overset{\hat{r}}{<}}d_1{\overset{\hat{r}}{<}}d_2{\overset{\hat{r}}{<}}d_4{\overset{\hat{r}}{<}}d_5$$
因此可以发现算法排序中有3对pair不一致了($\{d_2,d_3\}$,$\{d_1,d_2\}$,$\{d_1,d_3\}$),所以$Q=3$,$P=7$,最终的$\tau(r,\hat{r})=\frac{7-3}{10}=4$
$\tau$的值越大,表示排序效果越接近真实,比如上面的$\tau(r,r)=\frac{10-0}{10}=1$
RankSvm还证明了由$Q$的倒数正相关的一个式子为平均准确率指标的下界(具体证明看原文附录):
$$AvgPrec(\hat{r}) \geq \frac{1}{R} \left[Q+\binom{R+1}{2}\right]^{-1} \left(\sum_{i=1}^{R} \sqrt{i}\right)^2$$
$R$为排序出现的文档中与query相关文档数量(这个是Mean Average Precision中的标注,与Pair对的样本稍微有点差别)
从这个角度也可以看到$\tau$来衡量排序效果好坏的合理性.
假设现在有$n$个$q_i$作为训练样本,他们各自的目标排序为$r_i^*$,也就是:
$$(q_1,r_1^*),(q_2,r_2^*),(q_3,r_3^*),…(q_n,r_n^*)$$
其中算法排序为$\hat{r}_i$,则排序算法的优化目标是将下列式子
$$\tau_{s}=\frac{1}{n} \sum_{i=1}^{n}\tau(r_i^*,\hat{t}_i)$$
进行最大化.
RankSvm排序
假设能找到一个排序算法能使得上面的$\tau_s$得到最大化,对于一个指定的查询$q$,每个文档$d_i$使用特征向量映射方法$\Phi(q,d_i)$,如果是直接使用线性排序方法:
$$(d_i,d_j) \in \hat{r} \Leftrightarrow \vec{w} \Phi(q,d_i)>\vec{w} \Phi(q,d_j)$$
$\vec{w}$表示权重向量,线性排序下,排序分数为权重 x 特征向量
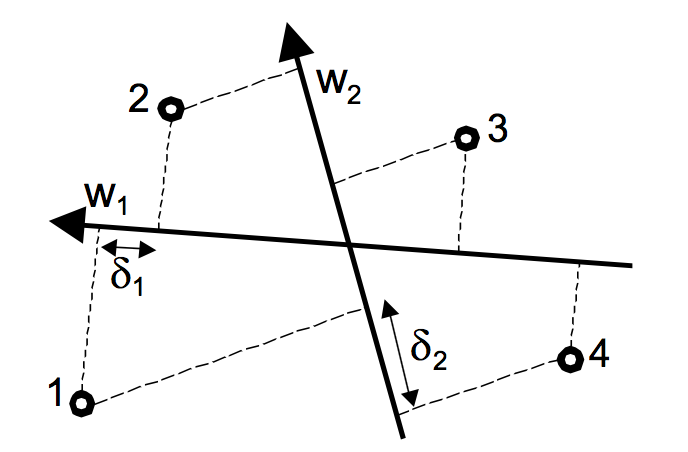
上图表示一个二维的
权重与特征图,在排序的顺序的就是特征在权重上的映射位置顺序,比如单从$W_1$维度进行观察可以看到的排序顺序为{1,2,3,4},而如果按$W_2$维度则是{2,3,1,4}。
为了最大化$\tau_s$,可以最小化$ Q$来代替,也就是说对于线性的排序,$Q=0$就是表示下面的等式全成立(也就是最大化)
$$
\forall (d_i,d_j) \in r_1^* : \vec{w} \Phi(q,d_i)>\vec{w} \Phi(q,d_j) \\
… \\
\forall (d_i,d_j) \in r_n^* : \vec{w} \Phi(q,d_i)>\vec{w} \Phi(q,d_j)
$$
不幸的是,优化这个是一个NP难题。
然而SVM在由于软间距最大时可以看到熟悉的身影:
minimize:
$$\frac{1}{2} \vec{w} \cdot \vec{w} + C \sum \xi_{i,j,k}$$
subject to:
$$
\forall (d_i,d_j) \in r_1^* : \vec{w} \Phi(q,d_i) \geq \vec{w} \Phi(q,d_j) + 1 - \xi_{i,j,1} \\
… \\
\forall (d_i,d_j) \in r_n^* : \vec{w} \Phi(q,d_i) \geq \vec{w} \Phi(q,d_j) +1 - \xi_{i,j,n} \\
\forall_i \forall_j \forall_k:\xi_{i,j,k} \geq 0
$$
$\xi$为松弛项,$C$表示平衡项
因此优化该问题时可以将约束转为:
$$\vec{w} \Phi(q,d_i)-\vec{w} \Phi(q,d_j) \geq 1 - \xi_{i,j,1}$$
并且由于是线性排序,可以进一步精简为:
$$\vec{w} \left(\Phi(q,d_i)-\Phi(q,d_j)\right) \geq 1 - \xi_{i,j,1}$$
在Pair对中只可能$d_i$是否排在$d_j$前面是一个二值结果,所以我们可以将$d_i$排在$d_j$前面的Pair为正标签,否则为负标签:
$$ y=\left\{
\begin{aligned}
+1 & \quad if \quad \vec{w} \Phi(q,d_i)>\vec{w} \Phi(q,d_j) \\
-1 & \quad otherwise\\
\end{aligned}
\right.$$
则最终可以将约束可以写成:
$$y_i \cdot \vec{w} \left(\Phi(q,d_i)-\Phi(q,d_j)\right) \geq 1 - \xi_{i,j,1}$$
其中传统的偏置项在
RankSvm是不需要的,以为正好Pair相减时就消掉了
这样就可以完全将上面构建的样本转为一个分类问题,使用SVM的对偶形式进行求解,并且还可以使用核函数进行非线性的分类^_^
训练完Svm之后,在正真排序时只需要将原始$doc$的特征向量输入Svm模型即可:
$$resv(q,d_i)= \vec{w} \Phi(q,d_i) = \sum_l^n a_{l}^*y_i(\Phi(q,d_i) \cdot \Phi(q,d_l)) $$
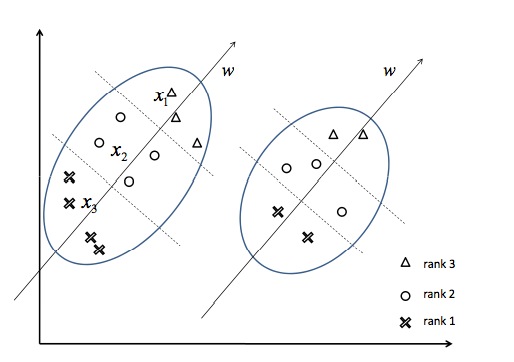
上面是表示两个不同的
query所表示的特征空间,不同的形状表示文档与对应query的相关性档位,三角形$x_1$表示相关性档位高,圆圈$x_2$表示相关性档位一般,叉叉$x_3$表示相关性档位差。将这些样本转为
Pair对之后可以有:
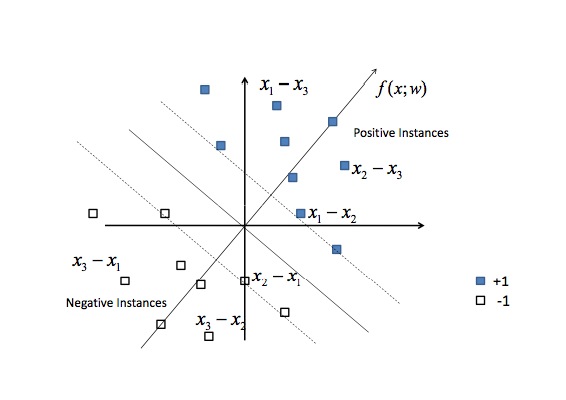
可以发现$x_1-x_3$和$x_1-x_2$为正样本,而$x_2-x_1$和$x_3-x_1$为负样本,因此可以形成对应的训练数据进行训练,其实这样形成的样本是对称的,因此在实际使用中一般只保留一侧即可。
总结
RankSvm很好的解决原始训练样本构建难的问题,根据点击日志构建样本,既考虑了doc之间的顺序,又保证了可持续性,并且其Pair对的训练正好可以使用Svm进行求最优化,而Svm分类器已经是非常成熟并且广泛使用的一种机器学习算法。
因此RankSvm虽然在2002年就提出,但是至今在工业界还是广泛使用,但是现在的主要难点是样本Pair对的构建,针对不同的场景也不同的策略,不一定只是根据点击顺序,实际使用中还要考虑新样本数据。
参考
- Joachims T. Optimizing search engines using clickthrough data[C]// Proceedings of the eighth ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2002:133-142.
- 《Learning to Rank for Information Retrieval and Natural Language Processing》.Hang Li
本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可,我的博客欢迎复制共享,但在同时,希望保留我的署名权kubiCode,并且,不得用于商业用途。如您有任何疑问或者授权方面的协商,请给我留言。

