聊聊机器学习中的损失函数
机器学习算法一般都是对损失函数(Loss Function)求最优,大部分损失函数都是包含两项:损失误差项(loss term)以及正则项(regularization term):
$$J(w)=\sum_iL(m_i(w))+\lambda R(w)$$
损失误差项
常用的损失误差项有5种:
Gold StandardHinge:Svmlog:logistic regression(cross entropy error)squared:linear regressionExponential:Boosting
Gold Standard Loss
Gold Standard又称0-1误差,其结果又称为犯错与不犯错,用途比较广(比如PLA模型),其损失函数也是相当的简单:
$$ y=\left\{
\begin{aligned}
0 & \quad if \quad m \geq 0 \\
1 & \quad if \quad m \le 0\\
\end{aligned}
\right.$$
Hinge Loss
Hinge的叫法来源于其损失函数的图形,为一个折线,通用函数方式为:
$$L(m_i) = max(0,1-m_i(w))$$
Hinge可以解 间距最大化 问题,带有代表性的就是svm,最初的svm优化函数如下:
$$\underset{w,\zeta}{argmin} \frac{1}{2}||w||^2+ C\sum_i \zeta_i \\
st.\quad \forall y_iw^Tx_i \geq 1- \zeta_i \\
\zeta_i \geq 0 $$
将约束项进行变形则为:
$$\zeta_i \geq 1-y_iw^Tx_i$$
则可以将损失函数进一步写为:
$$\begin{equation}\begin{split}J(w)&=\frac{1}{2}||w||^2 + C\sum_i max(0,1-y_iw^Tx_i) \\
&= \frac{1}{2}||w||^2 + C\sum_i max(0,1-m_i(w)) \\
&= \frac{1}{2}||w||^2 + C\sum_i L_{Linge}(m_i)
\end{split}\end{equation}$$
因此svm的损失函数可以看成L2-Norm和Hinge损失误差之和.
Log Loss
log类型损失函数的优势可以将连乘转为求和,由于是单调函数,不会改变原结果,并且还很方面求最优,因此log类型的损失函数函数也非常常用,比较著名的一种就是交叉熵(cross entropy),也就是logistic regression用的损失函数:
$$J(w)=\lambda||w||^2+\sum_i y_i log g_w(x_i)+(1-y_i)(log 1-g_w(x_i),y_i \in\{0,1\}$$
其中:
$$g_w(x_i)=\frac{1}{1+e^{-f_w(x_i)}} \\
f_w(x_i) = w^Tx_i
$$
Squared Loss
平方误差,线性回归中最常用:
$$L_2(m)=(f_w(x)-y)^2=(m-1)^2$$
Exponential Loss
指数误差,在boosting算法中比较常见:
$$J(w)=\lambda R(w)+\sum_i exp(-y_if_w(x_i)) \\
L_{exp}(m_i) = exp(-m_i(w))
$$
误差项对比
上面5种误差项的函数为:
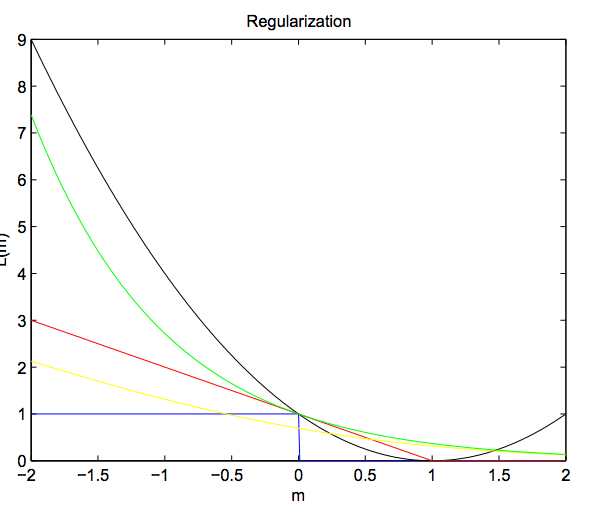
黑色为
Squared Loss,红色为Hinge Loss,黄色为:Log Loss,绿色为:Exponential Loss,蓝色为:Gold Standard
观察图中:
Hinge Loss中当$m_i(w) > 1$ 时,其损失项始终未0,当$m_i(w) < 1$时,其损失项的值呈线性增长(正好符合svm的需求).Squared、Log、Exponential三种损失函数已经Hinge的左侧都是凸函数,并且Gold Stantard损失为他们的下界:
$$\zeta_{01} \leq \hat{\zeta}_{01}(h)+fudge$$- 当需要求最大似然时(也就是概率最大化),使用
Log Loss最合适,但是一般会加上一个负号将其转换为求最小 - 损失函数和的
凸特征以及有界是非常重要的,可以防止在一些可以求得无穷的工作上白白浪费时间。有时候为了让函数有界和凸特征,一般会使用一些代理函数来进行替换。
正则项
加入正在项是为了降低模型复杂度,在一定程度上可以有效防止模型过拟合
常用的正则项有:
$$
R_2 = \frac{1}{2}||w||^2 \\
R_1 = \sum_i |w_i| \\
R_0 = |\{i:w_i \neq 0 \}|
$$
这些正则项可以通用的写成:
$$R_p =(\sum_i |w_i|^p)^{\frac{1}{p}}$$
其中:
- $R_2$最常用,因为它是凸函数,非常方便可以用
梯度下降法最优化 - $R_1$含有特征选择功能,因此经过$R_1$计算之后会有大量的0权重出现,这样的话我们在实际计算中只需要计算有值特征即可,可以加快速算法的运行速度
- $R_0$,额~这个暂时不知道哪里用-_-
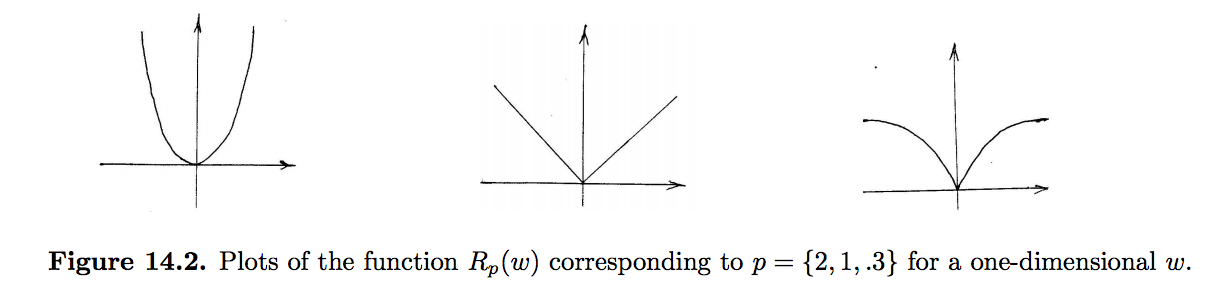
当$p \leqslant 1$时其正则项就为非凸函数了
参考
- http://www.ics.uci.edu/~dramanan/teaching/ics273a_winter08/lectures/lecture14.pdf
- https://www.wikiwand.com/en/Hinge_loss
- http://www.cnblogs.com/rocketfan/p/4081585.html
本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可,我的博客欢迎复制共享,但在同时,希望保留我的署名权kubiCode,并且,不得用于商业用途。如您有任何疑问或者授权方面的协商,请给我留言。

