AdaBoost学习总结
三个凑皮匠,顶一个诸葛亮,打一算法:AdaBoost
本文是自己对AdaBoost的理解,健忘-_-!! 故记录在此.
简介
痛点:大部分强分类器(LR,svm)分类效果还不错,但是可能会遇到过拟合问题,并且训练相对复杂,耗时~
另外大部分弱分类器(阈值分类器,单桩决策树(decision stump)等),他们分类的效果差,可能是极差,只会出现欠拟合,但是他们训练预测快,很快~
天下武功,唯快不破,做减法不易,但是做加法就相对简单了^_^ 这就是提升方法.
提升方法需要解决的两个问题:
- 在每一轮训练时如何改变数据的权值或概率分布?
- 如何将弱分类器组合成一个强分类器?
AdaBoost对此进行了很好的解决:
分而治之:将前一轮分错的样本加大权重,迫使在第二轮中对这些样本尽量分对,同时减少分对样本的权重.加权多数表决:加大错误率小的弱分类器的权重,使其在最终表决中占较大作用,同时减少错误率较大的弱分类器的权重.
前向分步算法
讲AdaBoost之前,就不得不提到前向分步算法,先来看一个加法模型:
$$f(x)=\sum_{m=1}^M \beta_m b(x;\gamma_m)$$其中:
- $b(x;\gamma_m)$表示基函数
- $\gamma_m$表示基函数的参数
- $\beta_m$表示基函数的系数
- 最终加权求和之后形成最终的函数(强模型)
假设损失函数为$L(y,f(x))$,则在训练$f(x)$时就是优化损失函数到最小化的问题:
$$\underset{\beta,\gamma}{min} \sum_{i=1}^N L\left( y_i,\sum_{m=1}^M \beta_m b(x;\gamma_m) \right)$$
如果直接优化这个损失函数无疑是一个相当复杂的问题:里面嵌入有太多了函数了…,而前向分步算法的策略是:
如果从前往后每一步都是学习一个基函数以及系数,令其逐步逼近优化目标函数,那么复杂度就可以大大简化了[分而治之]
因此每一步只需要如下的损失函数即可:
$$\underset{\beta,\gamma}{min} \sum_{i=1}^N L \left( y_i,\beta b(x;\gamma) \right)$$
下面就是前向分步算法的具体步骤:
Input:
- 训练数据集$T=\{(x_1,y_1),(x_2,y_2)…(x_N,y_N)\}$,其中$y_i \in \{+1,-1\}$
- 损失函数:$L(y,f(x))$
- 基函数数量:$M$
- 基函数集合$\{b(x;\gamma_m)\}$
Output:
- 加法模型$f(x)$
procedure:
- 初始化$f_0(x)=0$
- 循环$m \in \{1….M\}$
- 最小化基函数损失函数:$$\underset{\beta_m,\gamma_m}{argmin} \sum_{i=1}^N L\left( y_i,\beta_m b(x;\gamma_m) \right)$$
- 更新加法模型:$$f_m(x)=f_{m-1}(x)+\beta_m b(x;\gamma_m)$$
- 最终得到加法模型:$$f(x)=f_M(x)=\sum_{m=1}^M \beta_m b(x;\gamma_m)$$
前向分步算法通过分而治之的方式求得了损失函数值最小的加法函数
整个算法的学习过程可以有很大的想象空间^_^
AdaBoost算法逻辑
上面一小节介绍了前向分步算法,但是留下来三个问题:
- 对其损失函数$L(y,f(x))$有啥要求?
- 基函数的系数$\beta$又是怎么计算的?
- 基函数$b(x;\gamma)$如何设计比较合理?
AdaBoost正是对此进行一一填坑,它使用指数损失函数、根据分类错误类来计算基函数系数和 。。 基函数到没有指定,不过一般使用阈值函数或者单桩决策树来作为基函数
因此也可认为
AdaBoost是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法的二分类学习方法.
先来看下AdaBoost的算法逻辑图:
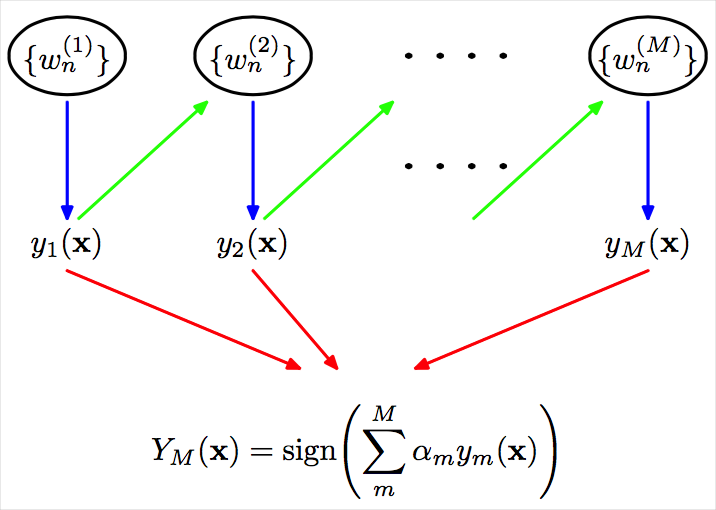
说明:此图来自
PRML Fig14.1[2],本文的数学符号主要采用[1]的风格,因此有:$y_m(x)\rightarrow G_m(x)$、$Y_M(x) \rightarrow G(x)$
从图中大致可以发现AdaBoost依次训练多个弱分类器,每个分类器训练完成之后产出一个权重给予下个分类器,下个分类器在此权重上继续进行训练,全部训练完成之后根据弱分类器的系数组合成强分类器,也就是最终的分类模型~
下面就是AdaBoost的具体步骤:
Input:
- 训练数据集$T=\{(x_1,y_1),(x_2,y_2)…(x_N,y_N)\}$,其中$y_i \in \{+1,-1\}$
- 弱分类器数量:$M$
- 弱分类器集合$\{G_m(x)\}$
Output:
- 最终模型$G(x)$ (注意:
产出的最终模型并不直接是加法模型哦~)
procedure:
- 初始化训练权值的分布:$$D_1=(w_{1,1},\cdot \cdot \cdot , w_{1,i},\cdot \cdot \cdot ,w_{1,N}),w_{1,i}=\frac{1}{N}$$
ps.其实初始化还有其他方式的 such as:初始化为$\frac{0.5}{N_+}$和$\frac{0.5}{N_-}$,其中$N_+$和$N_-$分别代表正负样本的数量,有$N=N_++N_-$
- 循环$m \in \{1….M\}$
- 使用带权重分布$D_m$的训练集进行训练,得到基本的弱分类器:$G_m(x)$
- 计算$G_m(x)$在训练数据集上的分类误差率:$$e_m=P(G_x(x) \neq y_i) = \sum_{i=1}^N w_{m,i} I(G_m(x_i) \neq y_i)$$其中$$ I(G_m(x_i) \neq y_i)=\left\{
\begin{aligned}
0 & \quad if \quad G_m(x_i) = y_i \\
1 & \quad if \quad G_m(x_i) \neq y_i\\
\end{aligned}
\right.$$其实就是
错误率:分错样本数量占总样本量的比例. - 计算$G_m(x)$的系数:$$\alpha_m = \frac{1}{2} ln \frac{1-e_m}{e_m}$$
- 更新训练数据集的权值分布(这点是核心):$D_{m+1}=(w_{m+1,1},\cdot \cdot \cdot , w_{m+1,i},\cdot \cdot \cdot ,w_{m+1,N})$
其中:$$w_{m+1,i} = \frac{w_{m,i}}{Z_m} e^{-\alpha_m y_i G_m(x_i)}$$ 这里$Z_m$为规范化因子:$$Z_m = \sum_{i=1}^{N} w_{m,i} e^{-\alpha_m y_i G_m(x_i)}$$
- 构建加法模型:$$f(x)=\sum_{m=1}^M \alpha_m G_m(x)$$产出最终的分类器:$$G(x)=sign(f(x))=sign\left( \sum_{m=1}^M \alpha_m G_m(x) \right)$$其中:$$sign(f(x))=\left\{
\begin{aligned}
-1 & \quad if \quad f(x) < 0 \\
1 & \quad if \quad f(x) \geq 0\\
\end{aligned}
\right.$$
对算法过程中几个重要的点进行一个简单的解释:
分类器误差率$e_m$对其权重$\alpha_m$的影响:
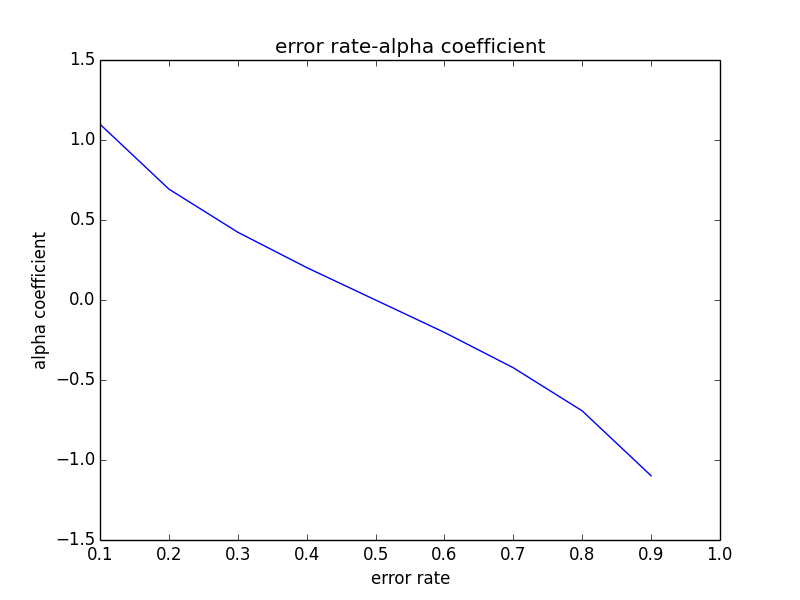
从图中可以发现:- $e_m$为0.5时其权重$\alpha_m$为0,表示此分类器在最终模型中不起任何作用
- $e_m < 0.5$时其$\alpha_m > 0$,表示对最终模型起正向作用,$e_m$的值越小,起到的作用越大
- $e_m > 0.5$时其$\alpha_m < 0$,表示对最终模型起父向作用,$e_m$的值越大,起到的负作用也越大
- $e_m$不会出现等于0 的情况,因为到了0的时候弱分类器已经全部分正确,也不需要继续更新权重再次训练了
- $e_m$也不会出现等于1的情况,因为1表示弱分类器全错,除了程序出问题,应该任何一个弱分类器不会训练到全错的情况吧^_^
数据权重的更新策略:
原始的更新策略是这样的:$$w_{m+1,i} = \frac{w_{m,i}}{Z_m} e^{-\alpha_m y_i G_m(x_i)}$$原始标签$y_i$和弱分类器结果的输出$G_m(x)$都是$\{+1,-1\}$二值,因此可以将上述更新方式写成:$$w_{m+1,i}= \left\{
\begin{aligned}
\frac{w_{m,i}}{Z_m} \times e^{\alpha_m} & \quad if \quad y_i \neq G_m(x)\\
\frac{w_{m,i}}{Z_m} \times \frac{1}{e^{\alpha_m}} & \quad if \quad y_i = G_m(x)\\
\end{aligned}
\right.$$观察$w_{m+1,i}$更新时三个元素均恒大于0($w_{m,i}$可以从$w_1$开始推),因此$w_{m+1,i}$也是恒大于0 ,并且$\sum_{i=1}^N w_{m,i}=1$
我们将分类错误率小于0.5的弱分类器称为好分类器,其系数$\alpha_{good}>0$,同时将分类错误率小于0.5的弱分类器称为坏分类器,则其系数$\alpha_{had}<0$,则再观察变形了的权重更新:
- 如果当前分类器是好分类器,样本$(x_i,y_i)$被错误分类时,$e^{\alpha_m} > 1$,其$w_{m+1,i}$将会被放大,反之正确分类样本的权值将会被缩小
- 如果当前分类器为坏分类器,样本$(x_i,y_i)$被错误分类时,$e^{\alpha_m} < 1$,其$w_{m+1,i}$将会被缩小,反之正确分类样本的权值将会被放大
这其实应该与误分类样本的权值被放大$e^{2\alpha_m}=\frac{e_m}{1-e_m}$倍一个道理,因为$\frac{e_m}{1-e_m}$不一定恒大于1啊~^_^
- 弱分类器的权重系数$\alpha_m$:
这个权重系数表示了弱分类器$G_m(x)$的重要性,但是$a_m$之和并不为1,另外$G_m(x)$输出的是-1或者1的分类,所以最终模型可以看做一个加权的投票系统^_^
AdaBoost-最小化指数误差
假如AdaBoost使用的是指数损失函数,则其损失函数为:$$L(y,f(x))=\sum_{i=1}^N e^{-y_if(x)}$$为了优化其损失函数,AdaBoost采用了前向分步算法进行逐步优化,第m轮的迭代需要得到的$\alpha_m$,$G_m$和$f_m(x)$,其中有$$f_m(x)=f_{m-1}(x)+\alpha_m G_m(x)$$,假设前面的$f_{m-1}(x)$已经为最优,则当前需要优化的是:
$$L(y,f_m(x))=\sum_{i=1}^N e^{-y_i(f_{m-1}(x)+\alpha_m G_m(x))}$$因为有$\bar{w}_{m,i}=e^{-y_if(x)}$(关于这个式子的成立并不是很理解-_-)所以上述优化目标可以写为$$L(y,f_m(x))= \sum_{i=1}^N \bar{w}_{m,i} e^{-y_i\alpha_m G_m(x)}$$
因为我们求的是关于$\alpha_m$和$G_m(x)$的最优化,所以$\bar{w}_{m,i}$相对来说就是常量了.现在假设第$m$轮迭代中有$T_m$个样本分类正确,有$M_m$个样本分类错误,则其优化目标又可以写为:
$$\begin{equation}\begin{split} L(y,f_m(x))&=e^{-\alpha_m} \sum_{n \in T_m} w_{m,n}+e^{\alpha_m} \sum_{n \in M_m} w_{m,n}\\
&= \left( e^{-\alpha_m} \sum_{n \in T_m} w_{m,n} + e^{-\alpha_m} \sum_{n \in M_m} w_{m,n} \right)+ \left( e^{\alpha_m} \sum_{n \in M_m} w_{m,n} - e^{-\alpha_m} \sum_{n \in M_m} w_{m,n} \right) \\
&= e^{-\alpha_m} \sum_{i=1}^N w_{m,i} + (e^{\alpha_m}-e^{-\alpha_m}) \sum_{n=1}^N w_{m,i}I(y_i \neq G_m(x_i))
\end{split}\end{equation}$$
接下来惯例的方法就是对$L(y,f_m(x))$求$\alpha$和$G_m(x)$的偏导数,其实在求$G_m(x)$最优时可以发现可以发现第一项和第二项前面的系数并不影响最优化,所以需要求的就是上面步骤中误差率的最优化:$$e_m=P(G_x(x) \neq y_i) = \sum_{i=1}^N w_{m,i} I(G_m(x_i) \neq y_i)$$
而得到了最优的$G_m(x)$之后代入$L(y,f_m(x))$求偏导又可以得到最小的$\alpha_m$为:$$\alpha_m = \frac{1}{2} ln \frac{1-e_m}{e_m}$$
又是一面熟悉的场景^_^
所以可以说AdaBoost整个过程是一直在优化最新函数的指数误差,只是在实际训练时按前向分步算法只需优化当前的误差率即可.
AdaBoost训练误差分析
这里的边界是我自己的理解,与[1]稍有区别
上一小节我们知道在每一步求$\sum_{i=1}^N w_{m,i} I(G_m(x_i) \neq y_i)$的最小化时,其实是在优化最终模型的损失函数$\sum_{i=1}^N e^{-y_if(x)}$,关于模型最终的损失函数有这样一个界限:
$$\frac{1}{N} \sum_{i=1}^N I(f(x) \neq y_i) \leq \frac{1}{N} \sum_{i=1}^N e^{-y_if(x)} = \prod_m Z_m$$
因为$e^{-y_if(x)}$一定不会小于0,并且当$f(x) \neq y_i$时,$e^{-y_if(x)}$恒大于1,因此第一、二项的不等式是成立的。接下来看后面的那个等式:
这里的推导需要用到$Z_m$的变形:$w_{m,i}e^{-\alpha_my_iG_m(x)} = Z_mw_{m+1,i}$
$$\begin{equation}\begin{split} \frac{1}{N} \sum_{i=1}^N e^{-y_if(x)} &= \frac{1}{N} \sum_{i=1}^N e^{-\sum_{m=1}^M \alpha_my_iG_m(x_i)} \\
&= \sum_{i=1}^N w_{1,i} \prod_{m=1}^M e^{-\alpha_m y_i G_m(x_i)} \\
&= Z_1 \sum_{i=1}^N w_{2,i} \prod_{m=2}^M e^{-\alpha_my_iG_m(x_i)} \\
&= Z_1 Z_2 \sum_{i=1}^N w_{3,i} \prod_{m=2}^M e^{-\alpha_my_iG_m(x_i)} \\
&… \\
&= Z_1 Z_2 … Z_{m-1}\sum_{i=1}^N w_{M,i} e^{-\alpha_My_iG_M(x_i)} \\
&= \prod_{m=1}^M Z_m
\end{split}\end{equation}$$
因此可以发现最优化(最小化)损失函数可以降低最终模型的错误率,同时其错误率与$Z_m$也是有关系的.
AdaBoost黑科技
Real AdaBoost
上面的AdaBoost的介绍中可以发现$G_m(x)$返回的是-1 或者1 (也就是直接离散值),其实这种方式的返回始终会有一定的gap,那么假如$G_m(x)$输出的是$p(x)=P(y=1|x)$,也就是$x$特征下输出值为1的概率.此时我们最优化的函数为:$$e^{-y \left(f_{m-1}(x)+G_m(p(x) \right)}$$而$G_m(x)=\frac{1}{2} ln \frac{x}{1-x}$
这种方式将会修复一定的gap,并且在某些实验中效果也是要好于直接离散的AdaBoost
提前终止
一般情况下是弱分类器训练$M$个才停止,而提前终止只是在训练多个层之后组成的最终分类器的结果已经小于一个置信度的误差,有一种方法可以加快这种判断:
- 一般训练数据里面负样本会远多于正样本
- 在多个级联的弱分类器在被训练之后,如果正样本被误分为负样本了,则人工将这样正样本进行标记并去去除(质量差的)
- 那么如果每一轮都是有50%的负样本被监测去重,那么久可以大大减小计算量
- 最终看假阳性和假阴性来判断是否终止
这种方式靠谱吗?要不就是我理解/翻译错了
这种提前终止的方法可以降低过拟合的可能性^_^
剪枝
剪枝指的是去除性能较差的弱分类器,提升效率。最简单的方法是:每个弱分类器都自己的系数和测试误差率极其分布,margineantu则提出的建议为:
- 弱分类器的选择应该分类多样性
- 如果两个弱分类器很相似,则可以将其中一个给去掉,同时增加相似弱分类器的系数(这里其实就是相当于剪枝了)
总结
AdaBoost秉承三个凑皮匠,顶个诸葛亮的原则,与其说AdaBoost是一个机器学习算法,我更觉得他应该是一个经典的机器学习框架,其优点有:
- 可以较为方便的控制过拟合(不能说避免过拟合,在弱分类器很强的情况下还真会过拟合的吧?看$GBRT$)
- 有非常强的自适应性
- 如果弱分类器很简单,则训练预测速度将会很快,毕竟最终复杂度是在弱分类器上乘以$M$
- 分类效果好,实现简单
- 可扩展性强~弱分类器可以随意换,甚至损失函数也可以换(比如换最小平方误差)
当然也有缺点:
- 相邻两个分类器训练有依赖关系,所以在并行实现下还是需要精心设计。
参考:
[1] 《统计学习方法》.李航.第八章
[2] 《Pattern Recognition And Machine Learning》.Christopher Bishop.chapter 14
[3] https://en.wikipedia.org/wiki/AdaBoost
本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可,我的博客欢迎复制共享,但在同时,希望保留我的署名权kubiCode,并且,不得用于商业用途。如您有任何疑问或者授权方面的协商,请给我留言。

