从Gradient Boosting 到GBT
本文大部分参考(译)自wiki[1]
如果说Gradient Boosting是一种机器学习算法框架的话,我想GBT(Gradient Boosting Tree)看做它的实现更为合适
Gradient Boosting原理
与其他
Boosting方法一样,Gradient Boosting通过迭代将弱分类器合并成一个强分类器的方法。
对于标准的$(x_i,y_i)$训练集,Gradient Boosting在迭代到第$m$次时,可能会得到一个分类能力不是很强的$f_m$模型,但是他下次迭代并不改变$f_m$,而是生成一个这样的新模型:$$f_{m+1} = f_m+G_{m+1}$$使得$f_{m+1}$较$f_m$而言拥有更为强大的分类能力,那么问题来了,这个$G_{m+1}$该如何训练呢?
现在假如训练完$G_{m+1}$可以得到完美的$f_{m+1}$,那么也就是有:$$f_{m+1} = f_m+G_{m+1}=y$$
这个式子可以写成$$G_{m+1}=y-f_m$$ 其中$y-f_m$表示上一次迭代得到分类器预测结果与真实结果的差值,我们一般称之为的残差(residual),因此也可以理解为Gradient Boosting在每一轮训练新的分类器将会拟合残差进行最优化
Gradient Boosting算法
假设现有训练集$\left\{ (x_1,y_1),(x_2,y_2)…(x_n,y_n) \right\}$,其中$x$是特征向量,$y$是相应的训练目标,在给定相应的损失函数$L(y,f(x))$,我们的目标是找到一个近似的函数$f(x)$使得与真实函数$f^*(x)$的损失最小期望值最接近:$$f^* = \underset{f}{argmin} E_{x,y} \left[ L(y,f(x)) \right]$$
Gradient Boosting方法假设$y$是一个实值,而$f(x)$近似目标函数是一个弱分类器$G_m(x)$加权求和的形式$$f(x)=\sum_{m=1}^M \gamma_mG_m(x)+const$$ 根据经验风险最小化的原则,近似函数$f(x)$将会尝试对训练集上的平均损失函数进行最小化,它从一个常量函数进行起步,并且通过贪心的方式进行逐步优化
$$
f_0(x) = \underset{\gamma}{argmin} \sum_{i=1}^n L(y_i,\gamma) \\
f_m(x) = f_{m-1}(x) + \underset{G \in H}{argmin} \sum_{i=1}^n L \left(y_i,f_{m-1}(x_i)+G_m(x_i) \right)
$$
然而,对于$L$为任意的损失函数时,在选择每一步最佳的$G_m(x_i)$时将会很难优化。
这里使用最速下降法(steepest descent)来解决这个问题
,在使用这种方法时,对于损失函数$L(y,G)$不要将其看做一个函数,而是将其看做通过函数得到的值的向量$G(x_1),G(x_2)…G(x_n)$,那么这样的话我们就可以将模型的式子写成如下的等式:
$$
f_m(x) = f_{m-1}(x) - \gamma_m \sum_{i=1}^n \triangledown_G L \left( y_i,f_{m-1}(x_i) \right) \\
\gamma_m = \underset{\gamma}{argmin} \sum_{i=1}^n L \left ( y_i,f_{m-1}(x_i)-\gamma \frac{\partial L(y_i,f_{m-1}(x_i))}{\partial G(x_i)} \right )
$$
上面第一个式子表示根据梯度的负方向进行更新,第二个式子表明了$\gamma$使用线性搜索进行计算。
下面就是具体的gradient boosting步骤:
Input:
- 训练数据集$T=\{(x_1,y_1),(x_2,y_2)…(x_N,y_N)\}$
- 可导的损失函数:$L(y,f(x))$
- 迭代的次数:$M$
Output:
- 最终模型$f(x)$
Procedure:
- 使用一个常量进行模型的初始化$$f_0(x) = \underset{\gamma}{argmin} \sum_{i=1}^n L(y_i,\gamma) $$
- 循环$m \in \{1….M\}$
- 计算残差$$r_{im}=-\left[ \frac{\partial L(y_i,f(x_i))}{\partial f(x_i)} \right]_{f(x_i)=f_{m-1}(x_i)} \quad i=1…n$$
- 使用训练集$\{ (x_i,r_{im}) \}$对弱分类器$G_m(x)$进行拟合
- 通过线性搜索进行乘子$\gamma_m$的计算$$\gamma_m = \underset{\gamma}{argmin} \sum_{i=1}^n L \left(y_i,f_{m-1}(x_i)+\gamma_m G_m(x_i) \right)$$
- 进行模型的更新:$$f_m(x) = f_{m-1}(x)+\gamma_m G_m(x)$$
- 输出最终的模型$f_M(x)$
下面是来自[2]中的对于不同损失函数下不同残差的计算
可以发现当损失函数为最小平方差时残差就是真实值与预测值的差值
Gradient tree boosting
提升树(Gradient tree boosting)故名思议就是使用决策树(一般使用CART树)来作为弱分类器.
提升树在第$m$步迭代时将会使用决策树$G_m(x)$来集合残差,现在假设这棵树有$J$个叶子节点,则决策树将会将空间划分为$J$个不相交的区域$R_{1m},R_{2m}…R_{3m}$,以及每个区域都是预测一个常量值,则树模型$G_m(x)$对于特征$x$的输入将可以写成$$G_m(x)=\sum_{j=1}^J b_{jm}I(x \in R_{jm})$$,其中$b_{jm}$表示每个区域的预测值,上面的介绍可以用下图来表示:
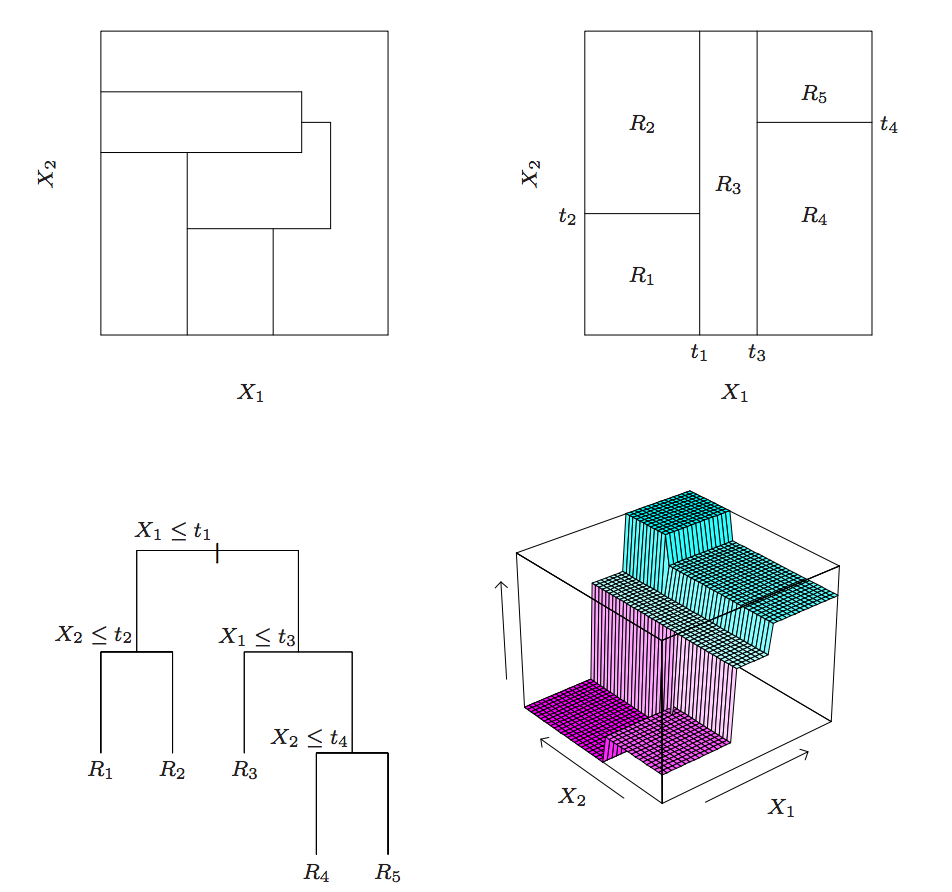
在实际使用时,$b_{jm}$也会与一个乘子$\gamma_m$相乘,最终模型的训练与上面一小节的介绍一致:
$$
f_m(x)=f_{m-1}(x)+\gamma_mG_m(x) \\
\gamma_m = \underset{\gamma}{argmin} \sum_{i=1}^n L \left(y_i,f_{m-1}(x_i)+\gamma_m G_m(x_i) \right)
$$
可以发现树的模型是关键,一般来时$4 \leq J \leq 8$比较合适,有时候$J=2$就足够了,并且$j > 10$比较少用
正则化
其实用过
Gradient Boosting的同学应该有同感,Gradient Boosting类型的模型(GBDT)调参很重要-_-,大致可以发现这些参数就是正则化的关键
调整树的个数
树的个数$M$越多,过拟合的情况可能越为严重,这里树的个数一般使用交叉验证的误差来调整确定
Shrinkage
Shrinkage又称学习率,是指在Gradient Boosting训练时不训练全部的残差,而是:$$f_m(x)=f_{m-1}(x)+v \cdot \gamma_mG_m(x) \quad 0 < v \leq 1$$
经验表明较小的学习率($v < 0.1$)将会取得较为明显的正则化效果,但是学习率太小会导致训练次数增加..
感觉这个大致可以这么理解,如果$v=1$,弱分类器犯错一次真的就错了,但是如果$v < 1$时,如果某个分类器犯错了,其他的的弱分类器可能还可以补救^_^
Stochastic gradient boosting
随机梯度提升法,表示每一轮迭代时并不是拿所有的数据进行训练,所以按无放回的随机取一定的比率$\eta$进行训练,这里的$ 0.5 < \eta < 0.8$将会取得较为不错的正则化效果,同时随机取样本进行训练还能加快模型的训练速度,并且每次迭代中未被抽中的样本还可以作为(out of bag)[https://en.wikipedia.org/wiki/Out-of-bag_error]进行估计
叶子节点的数量
一般这个叶子节点的数量不宜太多(其实可以理解为节点数越多,模型复杂度越高…)
使用惩罚项
额~貌似L2之类的惩罚项也是可以被加入进去
总结
Gradient Boosting是非常金典而又重要的提升方法,他与AdaBoost一样都是讲弱分类器合成强分类,但是其大致区别有:
Gradient Boosting通过残差来变量的改变错误分类的权重,而AdaBoost就真的直接去修改分类错误的训练权重了Gradient Boosting接入的分类器一般完整的决策树居多,但是AdaBoost一般使用二层决策树
Gradient Boosting中最有代表性的就是GBDT,该模型虽好,可不要贪杯~使用时理解数据以及正确调参才是王道
参考
[1]. wiki Gradient boosting
[2]. The Elements of Statistical Learning
[3]. 《统计学习方法》.李航.第八章
本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可,我的博客欢迎复制共享,但在同时,希望保留我的署名权kubiCode,并且,不得用于商业用途。如您有任何疑问或者授权方面的协商,请给我留言。

