RankNet是一种基于pairwise的学习排序,假设文档A以P的概率排在文档B的前面，则RankNet就是使用神经网络算法来使得这个概率最大化.last update at:2016-08-28

算法原理

假设现在有一对文档$D_i$和$D_j$,给定一个目标概率$\bar{P}_{i,j}$,以表示文档$D_i$将会排在文档$D_j$的前面.

1. 如果$\bar{P}_{i,j}=1$,表示$D_i$一定会排在$D_j$前面
2. 如果$\bar{P}_{i,j}=0.5$,表示$D_i$和$D_j$的前后关系将无法确定
3. 如果$\bar{P}_{i,j}=0$,表示$D_i$一定不会排在$D_j$前面

现在有一个实值的排序函数$f$,如果$f(x_i) > f(x_j)$，则会有$D_i \triangleright D_j$(表示$D_i$会排在$D_j$前面)

这里$x$是为文档$D$所表示的特征向量

我们现在将$P(D_i \triangleright D_j)$前后顺序的预测概率表示为$P_{i,j}$,同时定义$o_i \equiv f(x_i)$ 以及 $o_{i,j}=f(x_i)-f(x_j)$，则我们可以logistic函数来表示$P_{i,j}$:
$$P_{i,j} \equiv \frac{e^{o_{i,j}}}{1+e^{o_{i,j}}} \equiv \frac{1}{1+e^{-o_{i,j}}}$$

为了衡量预测概率$P_{i,j}$与期望/目标概率$\bar{P}_{i,j}$的接近程度，这里使用Cross Entropy作为损失函数:
$$C_{i,j} = -\bar{P}_{i,j} log P_{i,j} - (1-\bar{P}_{i,j}) log (1-P_{i,j})$$

将$P_{i,j}$代入损失函数$C_{i,j}$之后即可得到:
$$\begin{equation}\begin{split}C_{i,j}&=-\bar{P}_{i,j} log \frac{e^{o_{i,j}}}{1+e^{o_{i,j}}} - (1-\bar{P}_{i,j}) log (1-\frac{e^{o_{i,j}}}{1+e^{o_{i,j}}}) \\
&= -\bar{P}_{i,j} log \frac{e^{o_{i,j}}}{1+e^{o_{i,j}}} - (1-\bar{P}_{i,j}) log (\frac{1}{1+e^{o_{i,j}}}) \\
&= -\bar{P}_{i,j} \left( log \frac{e^{o_{i,j}}}{1+e^{o_{i,j}}} - log (\frac{1}{1+e^{o_{i,j}}}) \right) - log (\frac{1}{1+e^{o_{i,j}}}) \\
&= -\bar{P}_{i,j} o_{i,j} + log(1+e^{o_{i,j}})
\end{split}\end{equation}$$

下面的图是当$\bar{P}_{i,j} \in \{0,0.5,1\}$时的损失函数情况: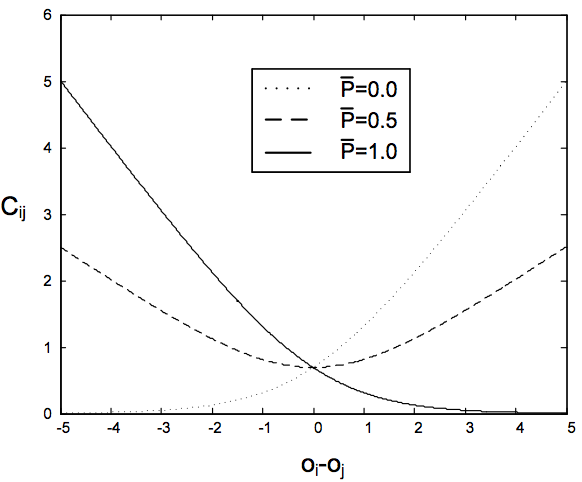

当$\bar{P}_{i,j} = 1$的时候，Cross Entropy的损失函数将会变为:$$C_{i,j}=log(1+e^{-o_{i,j}})$$
直接会变为一个log型的损失函数，其中$o_i-o_j$越大，损失函数的值也就会越小，这也是我们所期望训练的结果(表示我们的样本全部成立)

现我们损失函数$C_{i,j}$求$o$的偏导:
$$\frac{ \partial{C}}{ \partial{o_i}} = \left( -\bar{P}_{i,j}+\frac{e^{o_i-o_j}}{1+e^{o_i-o_j}} \right) =\left( -\bar{P}_{i,j}+P_{i,j} \right) = -\frac{ \partial{C}}{ \partial{o_j}}$$

其实可以发现就是在$-\bar{P}_{i,j}+P_{i,j}=0 $时就是我们的目标
另外请注意这里的$P_{i,j}$其实就是文献2中的$S_{i,j}$，但是由于他们的取值范围不一致 $P_{i,j} \in \{0,0.5,1\}$,$S_{i,j} \in \{-1,0,1\}$，因此导致了文献2中对于C的偏导与本文的有微小的偏差

现我们认为$w$为$o=f(x:w)$的一个权重,也就是我们最终希望求解的值，而这个参数我们就可以使用随机梯度下降法来求解:
$$w_k \rightarrow w_k - \eta \frac{\partial{C}}{\partial{w_k}} = w_k - \eta \left( \frac{\partial{C}}{\partial{o_i}} \frac{\partial{o_i}}{\partial{w_k}} + \frac{\partial{C}}{\partial{o_j}} \frac{\partial{o_j}}{\partial{w_k}} \right)$$

其中$\eta$表示学习率，一般取一个比较小的数（比如:$1e-3$,$1e-5$）
另外我们可以求得$C$的增量变化:
$$\Delta C = \sum_k \frac{\partial{C}}{\partial{w_k}} \Delta w_k = \sum_k \frac{\partial{C}}{\partial{w_k}} \left( - \eta \frac{\partial{C}}{\partial{w_k}} \right) = - \eta \sum_k \left( \frac{\partial{C}}{\partial{w_k}} \right)^2 < 0 $$

1. $\Delta C < 0 $表示随着权重参数$w$的沿着负梯度的变化，损失函数$C$会越来越小
2. 另外当梯度$\frac{\partial{C}}{\partial{w_k}} = 0$时，才会让损失函数达到最小值

上面的式子告诉我们通过梯度下降法求解RankNet时，就算算分函数没有好的梯度或者不可求导时任可以进行权重的更新（直接对$o$进行梯度下降，但是其梯度方向需要自己指定，并且要求权重$w$与最终的算法$o$是相关的）。

合并概率

理想的情况下，$\bar{o}$的输出得到的模型应该是这样纸的:$$\bar{P}_{i,j}=\frac{e^{\bar{o}_{i,j}}}{1+e^{\bar{o}_{i,j}}}$$

其中$\bar{o}_{i,j}=\bar{o}_i-\bar{o}_j$

上面的模型需要$\bar{P}_{i,j}$保持一致性，也就是如果$D_i$的相关性要高于$D_j$,$D_j$的相关性同时也是要高于$D_k$，则$D_i$的相关性也是一定要高于$D_j$，如果没有保持一致性，其实上面的理论就不好使了。。。
现给定$\bar{P}_{i,j}$和$\bar{P}_{j,k}$时会有:

$$\begin{equation}\begin{split} \bar{P}_{i,k}&= \frac{e^{\bar{o}_{i,k}}}{1+e^{\bar{o}_{i,k}}}\\
&= \frac{e^{\bar{o}_{i,j}e^\bar{o}_{j,k}}}{1+e^{\bar{o}_{i,j}e^\bar{o}_{j,k}}} \\
&= \frac{ \frac{e^{\bar{o}_{i,j}e^\bar{o}_{j,k}}}{(1+e^{\bar{o}_{i,j}})(1+e^{\bar{o}_{j,k}})} }{ \frac{1+e^{\bar{o}_{i,j}e^\bar{o}_{j,k}}}{(1+e^{\bar{o}_{i,j}})(1+e^{\bar{o}_{j,k}})}} \\
&= \frac{\bar{P}_{i,j} \bar{P}_{j,k}}{\frac{(1+e^{\bar{o}_{i,j}}+e^{\bar{o}_{j,k}}+e^{\bar{o}_{i,j}}e^{\bar{o}_{j,k}})+(2e^{\bar{o}_{i,j}}e^{\bar{o}_{j,k}})-(e^{\bar{o}_{i,j}}+e^{\bar{o}_{i,j}}e^{\bar{o}_{j,k}})-(e^{\bar{o}_{j,k}}+e^{\bar{o}_{i,j}}e^{\bar{o}_{j,k}})}{(1+e^{\bar{o}_{i,j}})(1+e^{\bar{o}_{j,k}})}} \\
&= \frac{\bar{P}_{i,j} \bar{P}_{j,k}}{1+2\bar{P}_{i,j}\bar{P}_{j,k}-\bar{P}_{i,j}-\bar{P}_{j,k}}
\end{split}\end{equation}$$

其中第一步是基于这个来的:$$\begin{equation}\begin{split}e^{\bar{o}_{i,k}}&=e^{\bar{o}_i-\bar{o}_k} \\
&= e^{\bar{o}_i-\bar{o}_j+\bar{o}_j-\bar{o}_k}\\
&= e^{\bar{o}_{i,j}+\bar{o}_{j,k}} \\
&= e^{\bar{o}_{i,j}}e^{\bar{o}_{j,k}}
\end{split}\end{equation}$$

当$\bar{P}_{i,j}=\bar{P}_{i,k}=P$时，其$\bar{P}_{i,k}$的取值情况为: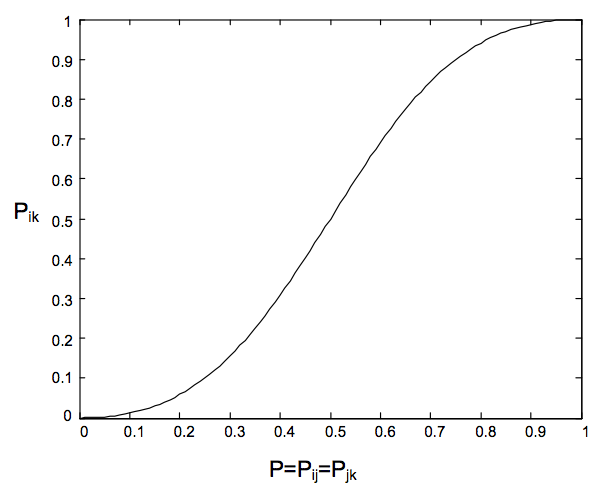

1. $P=0$时，有$\bar{P}_{i,k}=P=0$ 表示:$D_i$排$D_j$后面,$D_j$排$D_j$的后面，则$D_i$也一定排$D_j$的后面
2. $0 < P < 0.5$时，$\bar{P}_{i,k} < P$
3. $P=0.5$时，有$\bar{P}_{i,k}=P=0.5$ 表示:$D_i$有一般概率排$D_j$前面,$D_j$也有一半的概率排$D_j$的前面，则$D_i$同样也是一半的概率排$D_j$的前面
4. $0.5 < P < 1$时，$\bar{P}_{i,k} > P$
5. $P=1$时，有$\bar{P}_{i,k}=P=1$ 表示:$D_i$排$D_j$前面,$D_j$排$D_j$的前面，则$D_i$也一定排$D_j$的前面

从上面的图中可以看到，其实目标概率是都可以保持一致性的.

神经网络训练

RankNet使用的是一个2层的神经网络作为算分模型$f(x:w,b)$,他在排序分数的公式是:
$$o = f(x:w,b) = f^{(2)} \left( \sum_l w_l^{(2)} \cdot f^{(1)} \left( \sum_k w_{lk}^{(1)}x_k +b^{(1)} \right) +b^{(2)} \right)$$

其中:

1. $x_k$表示输入的$k$个特征元素
2. $w$表示每一层的权重,$b$表示每一层的偏置，上标$(\cdot)$表示当前所属的神经网络的层数
3. 下标$l$表示第一层的单元数量
4. $f$使用sigmoid作为激活函数

在对于上面的二层神经网络求解时:
$$\frac{\partial{C}}{\partial{b^{(2)}}} = \lambda_{i,j}({f’}_i^{(2)}-{f’}_i^{(2)}) = \Delta_i^{(2)} - \Delta_j^{(2)} \\
\frac{\partial{C}}{\partial{w^{(2)}}} = \Delta_i^{(2)}f_i^{(1)} - \Delta_j^{(2)}f_j^{(1)} \\
\frac{\partial{C}}{\partial{b^{(1)}}} = \Delta_i^{(2)}f_i^{(1)}w^{(2)} - \Delta_j^{(2)}f_j^{(1)}w^{(2)} \\
\frac{\partial{C}}{\partial{w_k^{(1)}}} = \Delta_i^{(2)} x_{i,k} - \Delta_j^{(2)} x_{j,k}
$$
这样神经网络就可以使用前向预测和后向反馈来进行训练了,只是其后向反馈阶段是需要通过pair进行计算的。

神经网络加速

这里我们输入的样本是pair对$\{(x_i,x_j),\bar{P}_{i,j}\}$,其中$\bar{P}_{i,j}$就是我们的目标概率,根据第一小节(算法原理)中指到的，使用梯度下降法进行求解:
$$\begin{equation}\begin{split} \frac{\partial{C}}{\partial{w_k}} &= \frac{\partial{C}}{\partial{o_i}} \frac{\partial{o_i}}{\partial{w_k}} + \frac{\partial{C}}{\partial{o_j}} \frac{\partial{o_j}}{\partial{w_k}} \\
&= \left( -\bar{P}_{i,j}+\frac{e^{o_i-o_j}}{1+e^{o_i-o_j}} \right) \left( \frac{\partial{o_i}}{\partial{w_k}} - \frac{\partial{o_j}}{\partial{w_k}}\right)\\
&= \lambda_{i,j} \left( \frac{\partial{o_i}}{\partial{w_k}} - \frac{\partial{o_j}}{\partial{w_k}}\right) \\
\end{split}\end{equation}$$

记$\lambda_{i,j} = \frac{\partial{C}}{\partial{o_i}} = -\frac{\partial{C}}{\partial{o_j}} = \left( -\bar{P}_{i,j}+\frac{e^{o_i-o_j}}{1+e^{o_i-o_j}} \right) $

上面的是对于每一对pair都会进行一次权重的更新，其实是可以对同一个query下的所有文档pair全部带入神经网络进行前向预测，然后计算总差分并进行误差后向反馈，这样将大大减少误差反向传播的次数，其更新的公式为:

$$\Delta w_k = -\eta \sum_{\{i,j\}\in I} \left(\lambda_{i,j} \frac{\partial{o_i}}{\partial{w_k}} - \lambda_{i,j} \frac{\partial{o_j}}{\partial{w_k}}\right) = -\eta \sum_i \lambda_i \frac{\partial{o_i}}{\partial{w_k}} $$

$I$表示某个query下所有不同排序的pair出现一次的集合，$\{i,j\}$表示两个文档满足$D_i \triangleright D_j$,也就是$\bar{P}_{i,j}=1$

这里要着重介绍一下$\lambda_i$:

$\lambda$可以理解为某个给定query（给定排序）下第$i$个文档$D_i$的一个值,为了计算$\lambda_i$，需要找到这个排序下所有排在$D_i$前面的文档$D_j$（此时有$\{i,j\} \in I$），以及所有排在$D_i$后面的文档$D_k$（有$\{k,i\} \in I$）,同时针对$\lambda_{i,j}$的文档进行累加，对于$\lambda_{k,i}$的文档进行累减.

比如 当前排序下只有一个pair,有$I=\{\{1,2\}\}$，则有$\lambda_1 = \lambda_{1,2} = -\lambda_2$
又比如，当前排序下有三个pair，有$I=\{\{1,2\},\{1,3\},\{2,3\}\}$,则有$\lambda_1 = \lambda_{1,2}+\lambda_{1,3}$、$\lambda_2 = \lambda_{2,3}-\lambda_{1,2}$、$\lambda_3 = -\lambda_{1,3}-\lambda_{2,3}$

对于表示成式子为:
$$\lambda_i = \sum_{j:\{i,j\} \in I} \lambda_{i,j} - \sum_{j:\{j,i\} \in I} \lambda_{i,j}$$

因此，我们可以认为$\lambda_i$为在某个给定query的$D_i$需要移动的方向以及移动的强度,另外这种方式可以看做是一种mini-batch的梯度下降算法，不要将全部的pair进行反向传播,其复杂度可以降到$O(n_q)$可以大大加快原始的神经网络训练.这也为LambdaRank奠定了基础（其实很多在LambdaRank的paper提出来的）

总结

RankNet训练希望文档pair对的前后排序概率与目标概率一致，用交叉熵作为损失函数，在实际排序中使用了神经网络作为算分排序函数，同时可以有min-batch的批量训练方法。据说微软的Bing之前使用着他.

参考

1. Burges, Chris, et al. “Learning to rank using gradient descent.” Proceedings of the 22nd international conference on Machine learning. ACM, 2005.
2. Burges, Christopher JC. “From ranknet to lambdarank to lambdamart: An overview.” Learning 11 (2010): 23-581.
3. Li, Hang. “Learning to rank for information retrieval and natural language processing.” Synthesis Lectures on Human Language Technologies 7.3 (2014): 1-121.

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。