文本相关性

在信息检索中文本相关性是排序因子中非常重要的一个特征，大部分的文本相关性特征是直接根据query和doc上的term进行各种匹配、各种计算得到的， 比如词频/频率、tf/idf/tf*idf、bm25、布尔模型、空间向量模型以及语言模型,今天看到参考[1]这篇paper，提到了可以将点击日志构成二部图,根据二部分进行向量传播，最终收敛之后进行文本相关性的计算，也算是比较新颖了，下文就主要是对该paper的一个学习以及自己理解的记录。
该paper提出的三个贡献:

1. 可以使query和doc在同一空间上生成词向量考虑
2. 对于未曾有点击行为的query和doc也可以进行该空间词向量的估计
3. 最终计算的效率较高，可以用于商业的搜索引擎

如果已知了query和doc在同一空间上的向量表示，这样文本相关性就可以直接使用相似度的计算方式来得到了~

已有点击行为的向量计算

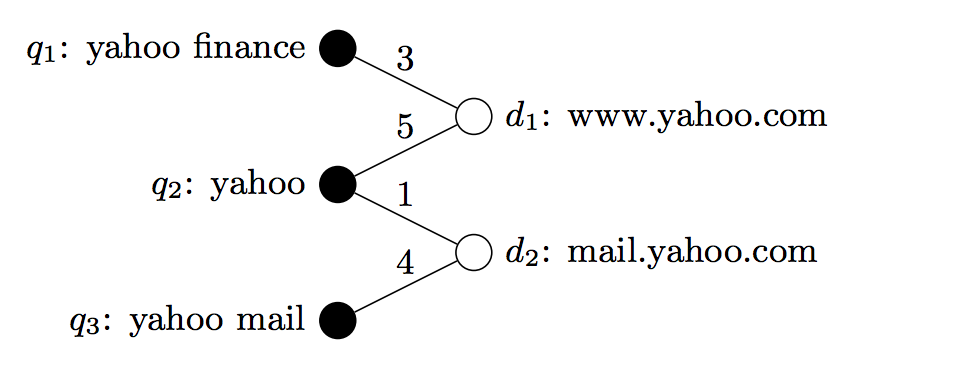
在搜索场景下用户输入query，对搜索的结果进行点击反馈，将所有用户的搜索行为收集起来之后可以形成一张大的Click-Graph，为了简单，我们使用二部分来表示，其中左侧为$Query$，右侧为$Doc$，如果$q_i$到$d_j$存在点击行为，则左右侧将会有一条边连接，连上的权重及点击的次数

现在假设语料的长度为$V$,则$Query$构成的矩阵为$|Query| \times V$，以及$Doc$构成的矩阵为$|Doc| \times V$，那么现在的任务就是如何计算这两个矩阵!

其实这个语料就是上面所说道的$Query$和$Doc$同处的向量空间,一般值$Query$里面抠出来的Term或者$Doc$里面的title/content抠出来的term.

这里使用的是向量传播来对$Query$和$Doc$进行计算，计算之前有这么这个假设:

1. 点击二部图上的边连接的$q_i$和$d_i$是有相关性的(或者说有较高的相关性)
2. $q_i$上的term与$d_i$上的title/content的term应该是存在联系的

目前暂不考虑缺少行为的$Query$和$Doc$，向量传播模型的步骤为:

1. 随意选择一侧进行向量初始化（$Query$和$Doc$端均可），我们使用$Query$向量来进行初始化$Q_i^0$,其中$Q_i^0$使用one-hot来表示，同时用$L2$进行归一化

   $i$表示第$Query$中的第$i$个,$0$表示第1次迭代（也就是初始化~）

2. 则第$D_j^n$个值($n>=1$)的更新根据被点击$Query$的向量进行加权求和即可:
   $$D_j^n=\frac{1}{||\sum_{i=1}^{|Query|}C_{i,j} \cdot Q_i^{n-1}||_2} \sum_{i=1}^{Query}C_{i,j} \cdot Q_i^{n-1}$$

   其中$Q_i^n$就是上一次迭代的$Query$向量，同样$D_j^n$也会进行一个$L2$正则化。

3. $Doc$的向量表示进行了一次迭代更新之后继续更新$Query$的向量，这里是根据$Query$下公共点击的文档信息进行更新，其方式与$Doc$的更新是一样的:
   $$Q_i^n=\frac{1}{||\sum_{i=1}^{|Doc|}C_{i,j} \cdot D_i^{n-1}||_2} \sum_{i=1}^{Doc}C_{i,j} \cdot D_i^{n-1}$$
4. 按2、3的步骤不断进行迭代，直至收敛，其产出的$Query$的$Doc$的向量就都在一个空间内，同时还可以计算相似度/相关性

这里以上的图为例再说一下计算过程:

1. 初始化$Query$的向量:
   • $Q_1:\{yahoo:\frac{1}{\sqrt{2}},finance:\frac{1}{\sqrt{2}},mail:0\}$
   • $Q_2:\{yahoo:1,finance:0,mail:0\}$
   • $Q_3:\{yahoo:\frac{1}{\sqrt{2}},finance:0,mail:\frac{1}{\sqrt{2}}\}$

     因为图中$Query$的语料三个term，所以这里初始化为3维.

2. 根据上一次$Query$的迭代信息以及与$Doc$的点击信息来更新$Doc$的向量:
   • $D_1=\frac{(\frac{3}{8}Q_1 + \frac{5}{8}Q_2)}{||\frac{3}{8}Q_1 + \frac{5}{8}Q_2||_2}$
   • $D_2=\frac{(\frac{1}{5}Q_2 + \frac{4}{5}Q_3)}{||\frac{1}{5}Q_2 + \frac{4}{5}Q_3||_2}$
3. 然后就是不断的迭代就行了，这样已经很清晰了

了解过一些信息检索或者链接分析的朋友可能会马上想到，咦~这好像Hits这个算法。的确是的，在计算过程中极为相似，不过Hits权重主要是计算Hubs与Authority两端的权重，而[1]中迭代完得到的是各个向量，有异曲同工之妙~
另外在实际的query量级一般都是百万以上，这样$Query$的语料的量就很大了,而搜索引擎中需要计算的性能要求极高，，所以一般进行稀疏存储，并且只取一些重要的term来对$Query$进行表示

缺少点击行为的向量计算

但是实际应用中用户搜索之后带来了点击行为的只是一小部分就，如果仅按照上述点击传播的方式来计算的话无query点击的文档将会将会无法得到正常的向量，同时一些新的$\hat{Query}$（从未有用户搜索过的query）也就无法得到正常的向量数据，所以需要一种对于这种缺失行为的$\hat{Query}$和$\hat{Doc}$进行向量表示估计.

由于在线计算相关性时对于已有行为的$Query-Doc$和缺失行为的是一视同仁的，因此为了在线计算时不应该因为训练数据产生偏差，所以需要与已有行为的$Qeury-Doc$向量在同一个空间内，同时考虑已有行为的$Query$和$Doc$的向量均已计算得到，我们还借助这些数据来预估缺失行为的向量.

提取Unit向量

既然未行为的$\hat{Query}$与$\hat{Doc}$之间没有任何边向量，那我们可以通过有行为的$Query$进行造边，先将$\hat{Query}$分解为各种Unit，这样就有$u_i \in unit(q_i)$,如果存在$Query$含有$u_i$，则将$u_i$对对应的$Query$之间形成一条虚拟的边,同时称含有$u_i$的所有$Query$的集合为$O_{u_i}$

这里分解时可以按n-gram进行分解，但是某个$Query$进行分解之后不能有overlap

这种边的构建方式如上图，$q_1$、$q_2$和$q_3$均都包含了yahoo这个词，则在他们之间形成这条虚线的边。
接下来我们可以理解$Query-Doc$之间的向量传播方法，我们当然也可以完成$Unit-Doc$的传播.
$u_i$会有$q_i$有边相连，而$q_i$与$d_i$又有变相连，因此我们可以间接认为$u_i$与$d_i$也是有边相连。
现假设$q_k$包含了$u_i$，同时$q_k$与$d_j$存在点击行为，$P_{i,k,j}$表示为这个二折线的权重，则该权重其实为$q_k$与$d_j$的点击次数，那么我们就会有
$$P_{i,j} = \sum_{k=1}^{|O_{u_i}|} P_{i,k,j}$$
其演示就是上图的右侧部分，yahoo与$d_1$之间的权重为8，与$d_2$之间的权重为5，既然到了这一步，我们就可以按照上一小节的传播方式来计算,这样就可以巧妙的得到$U_i$的向量:
$$U_i^n=\frac{1}{||\sum_{i=1}^{|Doc|}P_{i,j} \cdot D_i^{n-1}||_2} \sum_{i=1}^{Doc}P_{i,j} \cdot D_i^{n-1}$$

上面得到的是关于$\hat{Query}$上unit的向量，同样的我们也可以从$\hat{Doc}$这一侧出发，来计算$\hat{Doc}$
相关的unit

计算Unit向量权重

有了unit的向量之后，接下来要解决的问题就是如何得到$\hat{Query}$或者$\hat{Doc}$的向量了，其实最简单的方法就是将他们各自的unit进行平均即可,不过[1]使用线性回来来解决该权重问题，在进行权重训练时使用最小平方差:
$$\underset{w}{min} \sum_{i=1}^{|T|} || T_i-\sum_{u_j \in U_{T_i}^{all}} W_j \cdot U_j||_2^2$$

$T_i$是使用有点击行为的$Query$计算得到的向量，也就是我们所认为的gold-set
这样求出来的$W$就是各个$unit_i$不同的权重

预估向量

根据上面两个步骤得到的unit的向量和权重之后，得到整体的$\hat{Query}$或者$\hat{Doc}$就很方便了，由于unit本身就是$\hat{Query}$或者$\hat{Doc}$分解出来的，这里基础数据也都已经计算完成了，所以直接进行加权求和即可:
$$q_v=\sum_{u_i \in u_q} W_iU_i$$
和
$$d_v=\sum_{u_i \in u_d} W_iU_i$$

这样一来缺失形式的向量数据也都可以计算出来了

总结

该方法成功的借助了点击日志对于相关性进行估计（其实我觉得这种方式得到的文本相关性与ctr的预估会有部分重叠了），并且在实现上:

1. 已有点击数据的$Query$和$Doc$的向量直接离线就按完成
2. 缺失点击的$\hat{Query}$和$\hat{Doc}$可以利用离线计算的unit向量在线直接进行加权求和即可
3. 对于在线存储均使用稀疏方式并只存top-k，因此存储并不是问题
4. 在线计算相关性可以直接按相似度计算，复杂度为$k log k$所以并不是很高~

可实现性还是比较强的，但是对于一些未登录词就无能为力了….

关于改算法的最终实现结果去看paper吧，效果自然是还可以的

看了这篇paper，其实还是有点其他启发:

1. 如果搜索了query之后对于未点击的文档是不是可以进行降权（因为点击的文档是进行加权的）
2. 再想想，~其实直接使用来计算文本相关性风险还是挺大

参考

1. 2016-Learning Query and Document Relevance from a Web-scale Click Graph

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。