Federated Search 介绍¹

Federated search is an information retrieval technology that allows the simultaneous search of multiple searchable resources. —from WikiPedia

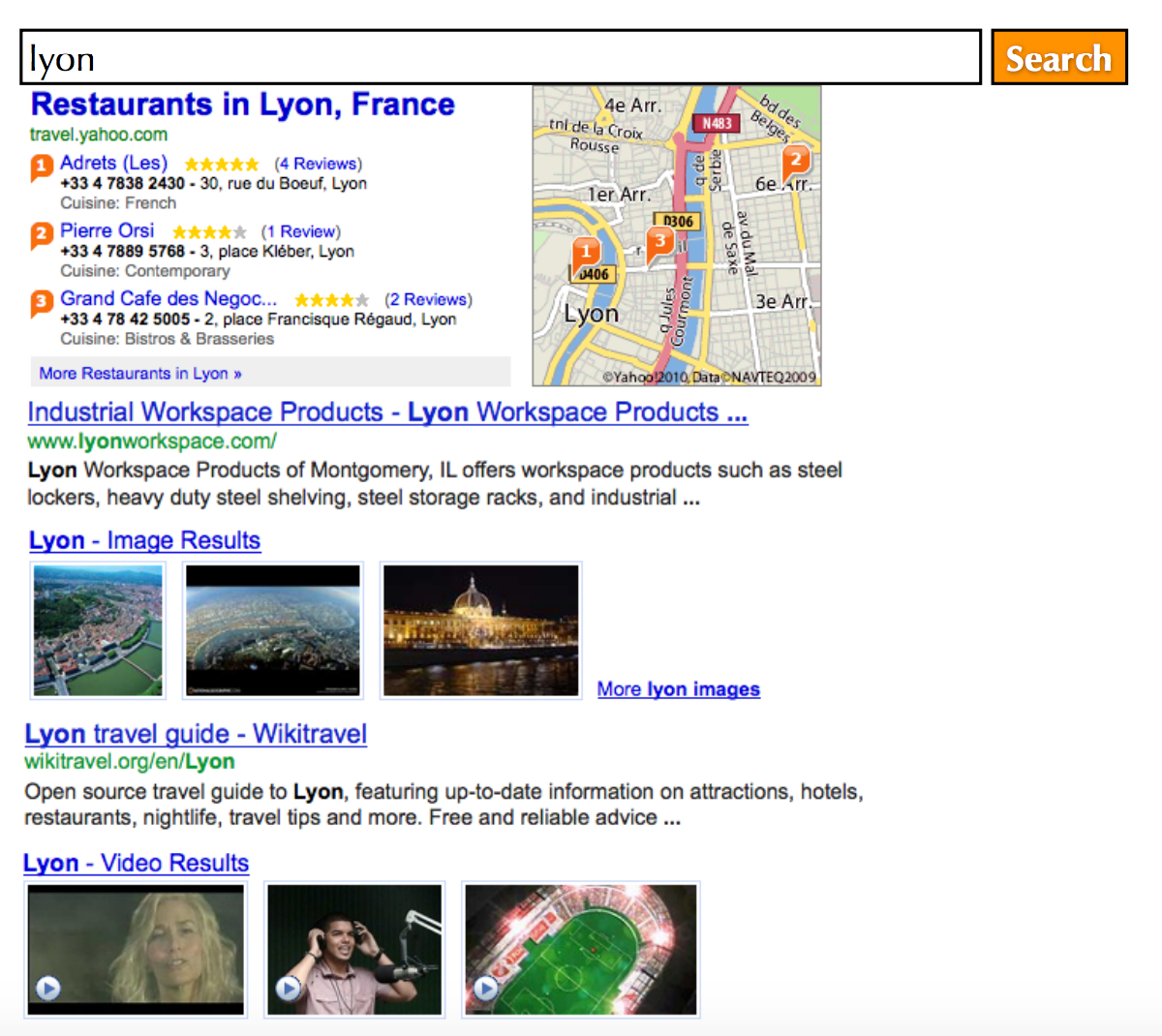
上图就是一个Federated Search的栗子，在搜索了lyon关键词之后有地图、图片、视频以及网页，其各种资源一般来说是不在同一个引擎的，其中召回排序算法也是不一致的，而Federated Search要做的就是接收到关键词之后给用户展现一个统一的界面。

下面就是Federated Search的链路架构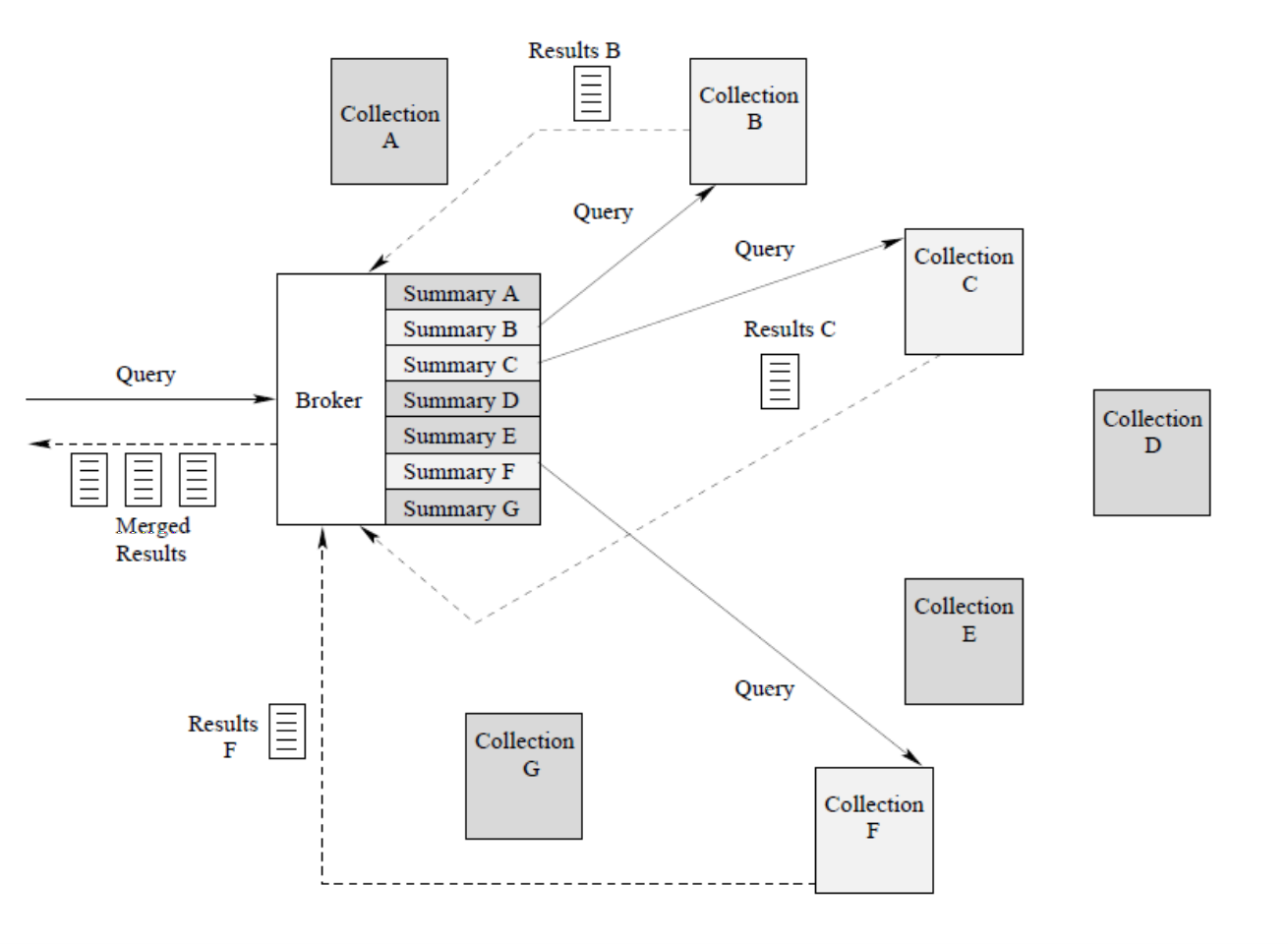

其Federated Search可以分解为两个任务:

1. Resource Selection:也叫Vertical Selection，就是选择不同的Vertical Resource去进行排序
2. Merge Result:也有叫Aggegate Content，在拿到不同Vertical之后进行合并排序

其中Resource Selection的难点有:

1. 待选择的Vertical可能是黑盒（比如第三方的引擎），没有里面细致的数据（这个点已经就很难了）
2. 待选择的Vertical一般都是异构的

另外Merge Result的难点有:

1. 各种Vertical出来都是异构的，也就是里面的特征会不一致
2. 就算特征一直，同特征的分布范围还不一致，所以无法用单一的模型去解决这个事情

[RS&MR]CORI²

CORI该算法包含了Resource Selection和Merge Result

在给定$Q$、观察到资源类别$C_i$,每个资源根据$P(Q|C_i)$来进行排序

$$T=\frac{df}{df+50+150*cw/avg\_{cw}} \\
I=\frac{log(|DB|+0.5)/cf}{log(|DB|+1.0)} \\
p(r_k|C_i)=b+(1-b)*T*I
$$

其中:

• $r_k$为$Q$中的第$k$个term
• $df$为资源$C_i$中包含$r_k$的文档数量
• $cf$为包含$r_k$的资源数量
• $|DB|$为需要排序的资源数量
• $cw$为在资源$C_i$中出现$r_k$的频次
• $avg\_cw$某个$C_i$的平均$cw$
• $b$默认值 一般为0.4

在合并的时候可以使用类似这种方式进行resultmerge:
$$C_i^{*} = \frac{(C_i-C_{min})}{(C_{max}-C_{min})} \\
D_i^{*} = \frac{(D_i-D_{min})}{(D_{max}-D_{min})}$$
最终归一化的score为(其实这儿就是做了一个映射):
$$D^{**} = \frac{D^{*} + 0.4*D^{*}*C_i^{*}}{1.4}$$

[MR]Semisupervised Learning(SSL)³

这个算法主要用于Merge Result阶段

用户在输入query时，希望会将该query分发到各个需要排序的引擎(database-specific)上面,此时同时会将query分发到一个中心的涵盖所有的资源的单独引擎上面(database-independent)

这个时候会出两个score:

1. database-specific-scorer:不同资源引擎排序的score，不同资源之间的维度不一样
2. database-independent -scroer：中心独立引擎上面，不同资源建所计算的score在同一个维度(估计这里只能用一个common的特征的排序)

同时会有讲个假设:

1. 同一个query出现在database-specific上面的大部分也会出现在database-independent中
2. database-specific与database-independent两者的overlap的doc拿到的score对使用机器学习方式可计算出一个映射

此时假设对于overlap的doc有如下score的pair对$s_{ind},s_{spe}$
需要做的就是使用线性回归的方式对两个score简建立一个映射
$$s_{ind} = w*s_{spe}+b$$
其需要优化的是:

$$argmin_w \sum_i (f(w,s_{spe})-s_{ind})^2$$

这样在各个混排引擎出来的时候就使用归一到同一纬度的score了，并且线性函数的运算很快
当然在训练数据不足的时候可以退化为CORI

但是他也有其他的缺点：

1. 需要额外维护一个中心引擎
2. 中心引擎出的score是同一纬度的算分，也是各个混排引擎的训练目标，但是如果他算分计算不准确，这个训练的结果将会很尴尬

[RS]REDDE⁴

主要是做Resource Selection，但是预先先做了Resource Sampling

Sample-Resample

首先需要使用sample-resample对未知的垂直资源进行一个数据量大小的估计:

1. 先从已采样的垂直资源中随机选几个query-term
2. 然后使用query-term再去请求垂直资源拿到返回的请求数以及top rank的部分doc

其中

• $C_j$表示某个垂直资源/数据库
• $\tilde{C}_j$表示该垂直资源的采样数据集
• $N_{C_j}$表示垂直资源里面的数据大小(条数)[未知]
• $N_{\tilde{C}_j}$表示采样垂直资源里面的数据大小条数
• $q_i$表示垂直资源中被选择出来的某个query term
• $df_{q_iC_j}$表示垂直资源$C_j$中包含$q_i$的文档数量（就是逆文档频次）
• $df_{q_i\tilde{C}_j}$表示采样垂直资源$\tilde{C}_j$中包含$q_i$的文档数量（就是逆文档频次）
• 事件$A$表示从垂直资源中采样的某个文档包含$q_i$
• 事件$B$表示垂直资源中某个文档包含$q_i$

则有:
$$P(A) = \frac{df_{q_i\tilde{C}_j}}{N_{\tilde{C}_j}} \\
P(B) = \frac{df_{q_iC_j}}{N_{C_j}}$$
假设采样可以很好的表示整个数据库/垂直资源，因此有$P(A) \approx P(B)$,则近似的有：
$$\hat{N}_{C_j} = \frac{N_{\tilde{C}_j} *df_{q_iC_j} }{df_{q_i\tilde{C}_j}}$$

最终是使用全部估计的均值来表示的

Resource Selection

在给定查询词$q$下对于$C_j$的相关性估计为:
$$\hat{Rel}_q(j) = \sum_{d_i \in C_j}P(rel|d_i) * P(d_i|C_j) * N_{C_j}$$

其中:

• $N_{C_j}$为资源$C_j$的总文档量，我们使用$\hat{N}_{C_j}$来近似
• $P(d_i|C_j)$这个概率将会是$\frac{1}{N_{C_j}}$

相应的，相关性的估计将可以被写为:
$$\hat{Rel}_q(j) = \sum_{d_i \in \tilde{C}_j} P(rel|d_i) \frac{1}{\tilde{N}_{C_j}} * \hat{N}_{C_j}$$

这样唯一剩下未知就是文档$d_i$与$q$的相关性了$P(rel|d_i)$
该paper并没有直接对其相关性做深入的研究，假如目前有一个中心数据库包含了所有的垂直资源，对其中心数据库来检索，则其相关性可以为:
$$P(rel|d_i)=\left\{
\begin{aligned}
C_q & \quad if Rank\_central(d_i) < ratio * \hat{N}_{all} \\
0 & \quad \text{otherwise} \\
\end{aligned}
\right.$$

其中:

• $Rank\_central(d_i) $为中心数据库中对于$d_i$的排序
• $ratio$为一个阈值，指示关注top多少的一个阈值(0.002~0.005表示合适)
• $\hat{N}_{all}$为中心数据中所有文档量的一个估计值
• $C_q$是一个独立于$q$的常量

这种完备的中心数据库其实建立起来不大可行，但是我们可以使用采样的中心数据库.
现在向采样的中心进行query检索，可以根据其返回结果来推断出实际中心数据库中各个文档的排序的位置:
$$Rank\_central(d_i) = \sum_{d_j | Rank\_S(d_j) < Rank\_S(d_i)} \frac{\hat{N}_{c(d_j)}}{\tilde{N}_{c(d_j)}}$$

这样最终$\hat{Rel}_q(j) $就可以计算出来了，最终在资源选择分布时可以按比例来:
$$\hat{Rank\_Rel}_q(j) = \frac{\hat{Rel}_q(j)}{\sum_i \hat{Rel}_q(i)}$$

[RS]Adaptation of Offline Vertical Selection⁵

原本最常用的垂直资源选择是使用one_vs_all的分类分类方法，其中$k$个垂直资源，这样就需要分$k+1$个类别，训练完预测的时候选择类别概率高的来进行展现

而这篇paper主要是在输入类别概率之后还将用户反馈加入了进来再计算:

Multiple Beta Prior

$p_q^v$可以用来表示某个Query下对于某个垂直资源类别v的相关概率，并且它是呈现beta分布的:
$$p_q^v \text{~} Beta(a_q^v,b_q^v)$$

其中$\pi_q^v$为离线模型概率，$\mu$为控制因子
$$a_q^v=\mu \pi_q^v \quad \quad b_q^v=\mu (1-\pi_q^v)$$

最后我们可以将相关性的后验写为
$$\tilde{p}_q^v = \frac{R_q^v + \mu \pi_q^v}{V_q^v + \mu}$$

$R_q^v$为$q$下展现$v$同时被点击的数量,$\bar{R}_q^v$表示展现了 但是未被点击的数量,$V_q^v$则表示一共展现的数量

Logistic Normal Prior

其先验为
$$p_q^v = \frac{exp(W_{tv})}{exp(W_{tv}) + exp(\bar{W}_{tv})}$$

$W$和$\bar{W}$是$t \times k$的随机矩阵，并且服从$W,\bar{W} ~ N_{2tk}(\eta,\sum)$,$\sum$为一个协方差矩阵

则其后验可以转为:
$$\tilde{p}_q^v = \frac{\pi_q^v exp(a_q^v)}{\pi_q^v exp(a_q^v) + (1-\pi_q^v) exp(b_q^v)}$$

最终关于$a_q^v,b_q^v$都是可以被计算出来的:
$$a_q^v = R_q^v+ \sum_{v’ \neq v} \frac{\sigma}{V_{q’}^{v’}} \bar{R}_q^{v’}$$
$$b_q^v = \bar{R}_q^{v’}+ \sum_{v’ \neq v} \frac{\sigma}{V_{q’}^{v’}} R_q^v $$
其中:

1. $R_q^v$表示$q$与$v$相关的对数
2. $V_q^v$表示$q$与$v$共现的总次数

Similar Queries

假设某个query1下知道他对于不同垂直资源的偏好，此时有一个query2与query1很相似，那么他关于垂直类目的偏好也会很相似
这个也是利用beta分布来估计的，算的是这个Bhattacharyya相似性，感兴趣自己去看paper

Randomizing Decisions

对于偏好概率很低的垂直资源也会有某个概率$\varepsilon $进行选择它，加了这个概率波动的之后，最后在选择垂直资源是这么计算的，其相关性为：$$P(v)=\frac{1}{Z} exp(\frac{\tilde{p}_q^v}{\tau})$$
它是符合Boltzmann分布,其中:

1. $\tilde{p}_q^v$为后验概率
2. $Z=\sum_vexp(\frac{\tilde{p}_q^v}{\tau})$
3. $\tau$是一个大于0的值，如果$\tau$趋向于正无穷，那么$P(v)$将会更加随机化，如果$\tau$接近于0，$P(v)$的选择将会更加贪婪（也就是哪个大选哪个）

[RS]Vertical Selection Evidence⁶

使用分类的方法来进行资源类别选择，里面讲的主要是各种特征

评估指标为:
$$P=\frac{1}{|Q|} \left( \sum_{q \in Q | V_q \neq \varnothing } I(\tilde{v}_q \in V_q) + \sum_{q \in Q | V_q = \varnothing } I(\tilde{v}_q = \varnothing) \right)$$

其中:

1. $V$表示所有垂直资源的集合
2. $Q$表示所有Query的集合
3. $V_q$为与某个$q$相关的垂直资源集合
4. $\tilde{v}_q$表示对于$q$预测的与其相关的一个垂直资源
5. $I(\cdot)$表示示性函数，应该就是${0,1}$的二值函数吧

下面是三大类特征Query String、Query Logs、vertical corpora:

1.Query String

该特征是为了利用Query中的一些关键短语与垂直资源的内容进行一些匹配

Rule-based vertical triggers(基于规则的触发)

文章中一共建立了45类别的属性来刻画query的垂直意图（其实就像类目，比如,local
phone, product, person, weather, movies, driving direction,
music artist）
同时这45类触发将会有三种规则：

1. 一对一触发:movies → movies, autos→ autos
2. 一对多触发:{sports players,sports} → sports, {product review, product} → shopping
3. 不显示对应：但是会提供一些positive或者negative的标志用于分类器,比如, patent, events, weather

里面的触发类别都是用过正则表达来提出取来，另外一个query可能关联到多个类别，一个触发器至少会匹配到一个query

Geographic features(地理特征)

在输入query下提取地理特征，并且会形成一个指定维护的概率向量:airport,colloquial,continent,town,等，将会与垂直资源中常常提到的这些地理词进行匹配

2. Query-Log Features

使用Query-log建立一个一元的语言模型
$$QL_q(V_i) = \frac{1}{Z}P(q|\theta_{v_i}^{qlog})$$
其中$\theta_{v_i}^{qlog}$为垂直资源$V_i$的语言模型，另外
$$Z=\sum_{v_j \in V}P(q|\theta_{v_j}^{qlog})$$

3.Corpus Features

垂直资源的语料特征

垂直资源采样

应该是这儿的垂直资源可能是分布到各种不同的引擎里面的（第三方），作者并无法取到全部的离线数据，所以在进行语料相关特征计算的时候需要拿到具有代表性的资源文档数据

在采样的时候使用垂直资源的top-query取访问垂直引擎，拿到文档再去统计，另一次关于垂直资源的语料去Wikipedia获取也是一种相当好的方式，因为里面都做好了结构化

基于语料的特征

1). Retrieval Effectiveness Features

$$Clarity_q(C) = \sum_{w \in V} P(w|\theta_q) \text{log} \frac{P(w|\theta_q)}{P(w|\theta_C)}$$

其中:

• $V$是垂直资源$C$的语料/word
• $P(w|\theta_q)$和$P(w|\theta_C)$分别是query和垂直资源的语言模型
  $$P(w|\theta_q) = \frac{1}{Z} \sum_{d \in R_{100}} P(w|\theta_d) P(w|\theta_d)$$
  $P(q|\theta_d)$为文本$d$的query似然分数，另外$Z=\sum_{d \in R_{100}}P(q|\theta_d)$

Clarity分数越小表示检索效果越差

最终各个资源也是按比例分数来计算的
$$Clarity_q^*(V_i) = \frac{1}{Z^*} Clarity_q(S_i^*)$$

2). ReDDE Features.
该Feature其实就是Luo.si 2003paper里面的计算方式
$$ReDDE_q^*(V_i) = |V_i| \sum_{d \in R_{100}} I(d \in S_i^*) P(q|\theta_d) P(d|S_i^*)$$
其中
$$P(d|S_i^*) = \frac{1}{S_i^*}$$

3). Soft.ReDDE Features
使用Bhattacharyya correlation
$$B(d,V_i) = \sum_{w \in top query}\sqrt{P(w|\theta_d) P(w|\theta_{V_i})} $$
其中
$$\phi(d,V_i) = \frac{B(d,V_i)}{\sum_{V_j \in V}B(d,V_j)}$$
最终soft针对文档的$B$进行求和，同时使用$P(q|\theta_d)$来加权:
$$Soft.ReDDE_q(V_i) = \sum_{d \in R_{100}} \phi(d,V_i) \times P(q|\theta_d)$$

Soft.ReDDE有两大好处：

1. 每个文档在他的资源类别排序中多多少少都有贡献
2. 不需要手动做文档到资源类别的映射(这个不懂….)

4). Categorical Features
最大熵求取多级类目特征

[MR] Aggregate Vertical Results⁷

Aggregate Vertical Results(就是最终多源搜索结果的合并)有两大难处：

1. 不同来源的特征不一致
2. 就是特征一直，同一个特征的值的分布也是不一致的

因此无法直接使用一个ML算法去学习他们的排序,需要一种算法去学习这种不一致的特征排序任务（好像是用了某些特征关系映射）
整个Aggregate Result有如下的假设:

1. 相同的垂直资源应该是被排到一起的
2. 垂直资源只能被嵌入到指定的坑位
3. 网页结果往往都是主排序
4. 不同的垂直资源是需要有关联的（这个有点难吧）
5. 我们假设用户不会去看那些不相关的垂直资源

这儿做的叫做block-rank坑位排序，比如有坑位1~3(w1)、4~6(w2)、7~10(w3)等，其中任务是预测排序顺序$\sigma(q)$与$\sigma^*(q)$尽量相似，其相似度可以使用$\text{Kendall’s} \tau$ 来衡量。
另外为了防止某些不相关性的block也被展现，所以有一个叫做end of search result(eos)的模块，如果被预测到这个模块，将会被放置到最下面并且不会展现

先说一下ML所使用到的特征Pre-retrieval Features和Post-retrieval Features

1) Pre-retrieval Features

在检索到垂直引擎之前的提取的特征

• Named-Entity Type Features
• Category Features.
• Click-through Features
• Vertical-Intent Features.(这个意图识别还是较难较重)

2) Post-retrieval Features

这个为在检索到垂直引擎之后提取的特征

• Hit Count Features:垂直引擎的召回量
• Temporal Features:时间性相关的特征（时效性）
• Text-Similarity Features.

BLOCK-RANKING APPROACHES

下面是实际的排序方法了

1) Classification Approach
每个垂直资源都有一个自己的分类器(这是使用的LR这个二分类器)
这里每个坑位都有一个阈值(除上面w1~3之外，还有一个eos的w4)
预测的是这个概率:
$$P(\sigma_q(v) < \sigma_q(eos))$$
也就是是否要被展现的概率，最终按这种方式进行填坑
$$P(\sigma_q(v) < \sigma_q(eos)) > \tau_y \forall x<y $$
这样就可以填入x坑位了（$\tau_y$是1~4坑位的阈值）

2) Voting Approach
这里也是使用独立的分类模型,但是他的分类对象是
$$P(\sigma_q(i)) < P(\sigma_q(j))$$
也就是pair，预测垂直资源$i$是否排在$j$前面，同时由于不同资源特征的限制,不同的$i,j$比较都是需要单独训练一个模型，最终使用投票的方式来确定哪个排在前面

这种方式将会训练大量模型，虽然paper中将某些block因素归一了，但是训练的模型量还是巨大的

3) Learning to Rank Approaches
使用RankSvm进行排序,但是会遇到不同类别的特征体系不一致的问题，通过下面三种方式解决

1. Equally Correlated Features:针对部分common特征可以合并起来
2. Uniquely Correlated Features.:对类别相关的特征进行copy和平铺出来，比如不同类别下同一个相关性特征可能会写两遍，但是都是时间特征在某些类别下只需要写一遍
3. Equally and Uniquely Correlated Features.:结合上面两种特征

但是上面的操作可能会导致过拟合，所以需要比较多的训练样本

[MR]Merging Multiple Result Lists⁸

用LambdaMerge的方法，其中好多使用了DNN，其框架为:

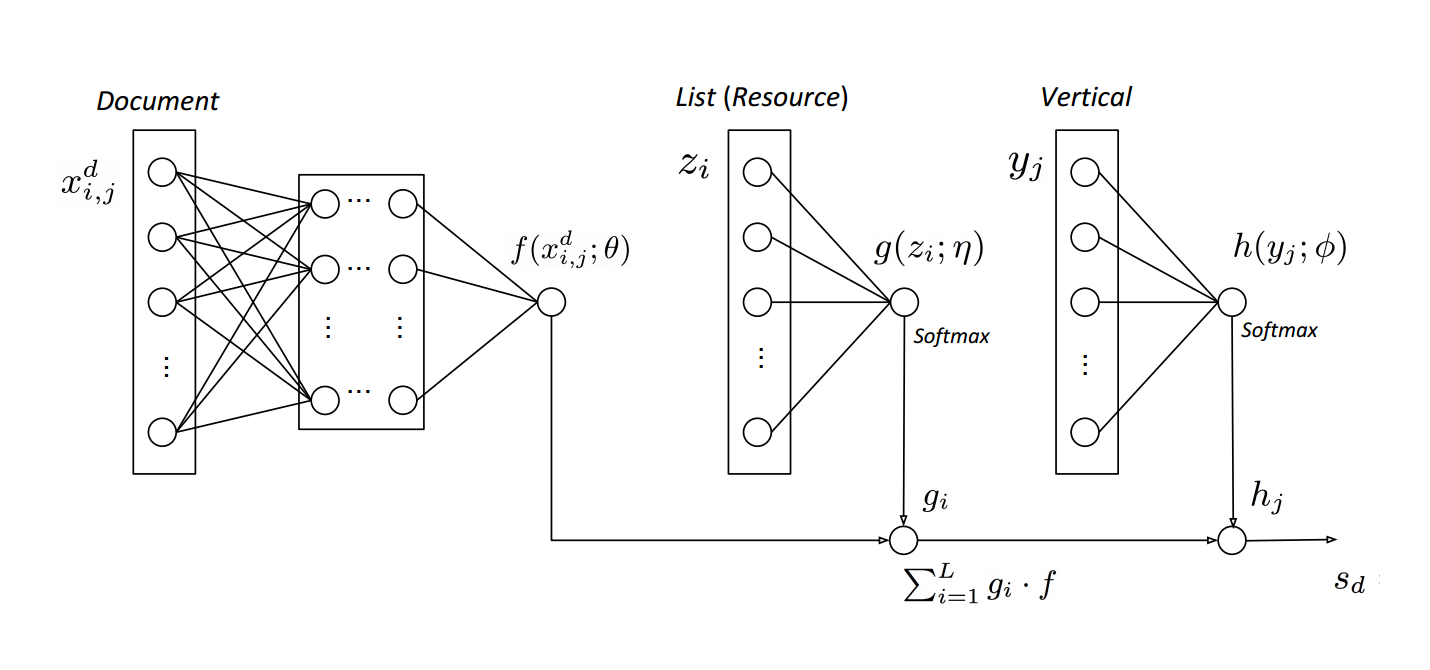
其中

• $f(x_{i,j}^d;\theta)$为文档相关的算法，前面那层的DNN,$x_{i,j}^d$为文档特征
• $g(z_i;\eta)$为不同搜索引擎相关的特征（比如google、bing等）,$g(z_i;\eta)$也搜索引擎相关的特征,也是用DNN过了一层
• $h(y_j;\phi)$为不同资源相关的特征,$y_j$为特征，也用dnn过了一层

最终使用lambdarank来解，感觉这种方法写paper可以，但是实际使用起来代价有点高的

[MR]Federated Search at LinkedIn⁹

这篇文章讲了混排在LinkedIn的实践，虽然没有高深的算法，但是讲的实在

在Linked中的，混排的对象有Job、People、Companies、post等，但是没有一个主要的排序对象（web search中一般网页都是主要排序对象）
下面是他们的混排框架

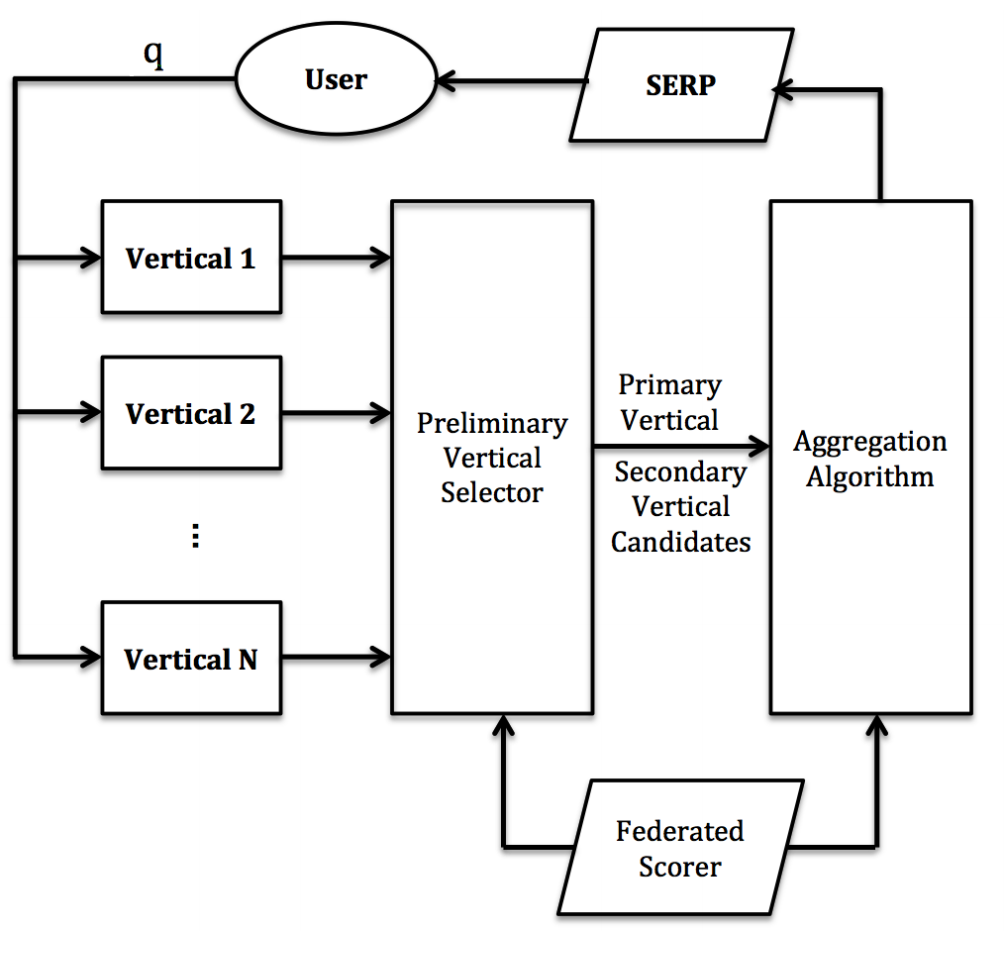
1. 用户输入一个query
2. 希望向各个垂直引擎进行请求
3. 请求完了之后各自引擎算完相关性得到top result（用LR进行计算的）
4. 根据top result中各个得分选出主要的资源P,其他的资源都称为C
5. 里面会对P和C的混排分进行一个归一化(没有细讲)
6. 然后以$P_i$为主，将其$C_i$与$P_i$比大小进行插入完成混排

其中排序选取的特征有:

1. Searcher Intent:用户自身的意图（稳定的，一天跑一把）
2. Keyword Intent:query的意图 实时概率预测
3. Base Ranking Features：基础特征了

整个算法简单粗暴，效果还可以，主要实现起来快，而且各个大引擎主要跑一次

[RS]2013-TREC¹⁰

2013年TREC比赛上关于Resource Selection的一些做法

resource selection-Krisztian Balog

使用语言模型进行估计:
两种方式，将一种资源统一看成一种文档:
$$P(q|c) = \prod_{t \in q}\left\{ (1-\lambda)\left(\sum_{d \in c}P(t|d)P(d|c)\right) + \lambda P(t)\right\}^{n(t,q)}$$

• $t$为$q$中出现的term
• $n(t,q)$表示$q$中出现$t$次数
• $P(t|d)$和$P(t)$为给定文档下面的最大似然估计
• $\lambda$为平滑因子
• $P(d|c) = \frac{1}{|c|}$看成均匀分布式

另一种方式是看一种资源看成多个文档
$$P(q|c) = \sum_{d \in c} P(d|c) \prod_{t \in q} \left( (1-\lambda)P(t|d)+\lambda P(t) \right)^{n(t,q)}$$

最终将两个分数进行一个合并
$$P(q|c) = \beta P_{cc}(q|c) + (1-\beta)P_{dc}(q|c)$$

resource selection-Emanuele Di Buccio

使用两个因子:

1. Inverse Resource Frequency (IRF) 类似逆文档频率
   $$IRF_t^{(z)} = \text{log} \frac{N^{(z)}}{n_t^{(z)}}$$

• $t$表示term
• $N^{(z)}$表示在$z$级别包含$t$的量
• $n_t^{(z)}$表示具体某个资源包含$t$的量

关于$z$有是有三个级别:: (1) document, (2) search engines and (3) the set of search engine

1. Term Weighted Frequency (TWF)
   $$w_{i,t}^{(z)} = TWF_{i,t}^{(z)} \cdot IRF_t^{(z-1)} $$
   同时
   $$TWF_{i,t}^{(z)} = \sum_{r \in R_i^z} TWF_{i,t}^{(z-1)} \cdot IRF_t^{(z-1)}$$

这儿是一个递归的方式

[RS]2014-TREC-Federated Search¹¹

2014年TREC比赛上关于Resource Selection的一些做法

1.resource selection - Qiuyue Wang

使用LDA来进行Resource和query的分布
由于query很短，作者的处理是用query查询google api取得top 50的文档的摘要，用组成的摘要来训练LDA，最终使用KL距离来衡量相似性

总结

看了一些Federated Search相关的Paper（当然还有两个综述也讲的很好[12],[13]），其中

• Resource Selection主要从统计学、相似度计算、概率生成模型以及分类模型来完成
• Merge Result有使用多源归一化，回归模型、LTR模型来完成，同时在算分最后大多使用Slot Filling的方法来做

Resource Selection目前的方法中好的Resource将会被更多的选择则，该阶段尝试加入Bandit相关策略也许会有比较好的效果,
另外Resource Selection和Merge Result目前在优化中其实并没有太大的联系，有没有可能有一种方法能将两个阶段联合起来进行全局优化?

参考文献

1. Arguello, Jaime, Fernando Diaz, and Milad Shokouhi. “Integrating and ranking aggregated content on the web.” Proc. WWW 2012 (2012).
2. Callan, James P., Zhihong Lu, and W. Bruce Croft. “Searching distributed collections with inference networks.” Proceedings of the 18th annual international ACM SIGIR conference on Research and development in information retrieval. ACM, 1995.
3. Sushmita, Shanu, et al. “Factors affecting click-through behavior in aggregated search interfaces.” Proceedings of the 19th ACM international conference on Information and knowledge management. ACM, 2010.
4. Si, Luo, and Jamie Callan. “Relevant document distribution estimation method for resource selection.” Proceedings of the 26th annual international ACM SIGIR conference on Research and development in informaion retrieval. ACM, 2003.
5. Diaz, Fernando, and Jaime Arguello. “Adaptation of offline vertical selection predictions in the presence of user feedback.” Proceedings of the 32nd international ACM SIGIR conference on Research and development in information retrieval. ACM, 2009.
6. Arguello, Jaime, et al. “Sources of evidence for vertical selection.” Proceedings of the 32nd international ACM SIGIR conference on Research and development in information retrieval. ACM, 2009.
7. Arguello, Jaime, Fernando Diaz, and Jamie Callan. “Learning to aggregate vertical results into web search results.” Proceedings of the 20th ACM international conference on Information and knowledge management. ACM, 2011.
8. Lee, Chia-Jung, et al. “An Optimization Framework for Merging Multiple Result Lists.” Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. ACM, 2015
9. Arya, Dhruv, Viet Ha-Thuc, and Shakti Sinha. “Personalized Federated Search at LinkedIn.” Proceedings of the 24th ACM International on Conference on Information and Knowledge Management. ACM, 2015.
10. http://trec.nist.gov/pubs/trec22/trec2013.html
11. http://trec.nist.gov/pubs/trec23/trec2014.html
12. Shokouhi, Milad, and Luo Si. “Federated search.” Foundations and Trends in Information Retrieval 5.1 (2011): 1-102.
13. Kopliku, Arlind, Karen Pinel-Sauvagnat, and Mohand Boughanem. “Aggregated search: A new information retrieval paradigm.” ACM Computing Surveys (CSUR) 46.3 (2014): 41.

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。