初识递归神经网络-RNN
RNN是啥?
当需要处理一些输入或者输出有相互依赖的任务时,传统的神经网络已经不再适用,比如在Language Model中在给定几个单词的情况下来预测下面将会出什么单词的时候。
这时候RNN就有用武之地了,RNN在预测/训练当前节点的时候可以获取前面节点的记忆(memory)信息,这样就可以很自然的完成序列任务的学习了。
一图胜千言,经典的RNN结构是长这样纸的:
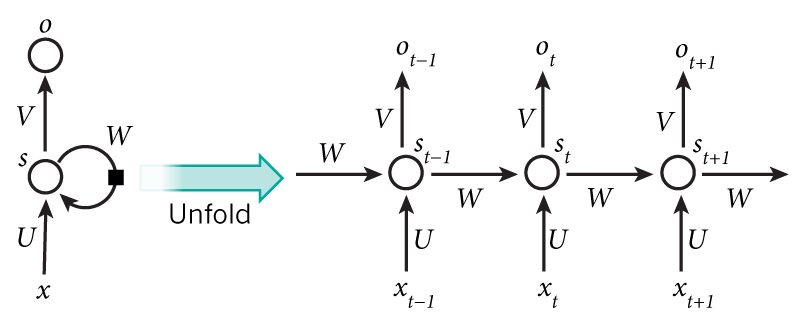
上图的左侧是一个未展开的RNN结构图,可以看出通过W来完成一个自循环,将其展开之后就很好理解了,展开后可以看做是一个横向的神经网络,每一层都有一个自己的输入,RNN的整个训练或者主要是为了计算U、W、V这三个矩阵,其训练时前向传播的步骤如下:
- $x_t$表示第$t$层/步的输入,输入的数据可以是一个
one-hot的向量或者一个其他的pre-train的向量 - $s_t$表示当前$t$的隐含状态,也就是整个网络中拥有
记忆的那一块,他是根据上一层的隐含状态$s_{t-1}$以及当前层的输入$x_t$计算得到的,$s_t=f(Ux_t+Ws_{t-1})$, 其中$f(\cdot)$为激活函数,一般可以为tanh或者ReLu,另外$s_{-1}$为初始化的隐含状态,一般来说可以都初始化为0 - $o_t$就是每一步的输出了,计算公式为$o_t = f(Vs_t)$,比如在
Language Model中每一步的输出就是预测到下一个词的概率,这输出的就是在vocabulary维度的一个概率向量$o_t=\text{softmax}(Vs_t)$
另外还有几点要说的:
- $s_t$为整个网络的记忆,但是在实际中,$s_t$的记忆功能是有限的,并不能捕捉$s_t$步之前的全部信息
- 在传统的深度神经网络中,每一层都有自己的参数,但是RNN与之不同,所有层之间都是共享
U、W、V这三个参数的 - 另外关于输出,上面说到的是每一层是一个输出,但是并不是非得这样,有一些其他的变种可以仅在最后一层有一个输出。
RNN的训练
将RNN进行展开之后可以看做一个横向的神经网络,因为RNN也可以按神经网络的方式进行训练和预测,这里以一个实际的语言模型来回顾一下RNN的前向预测:
- $s_t= \text{tanh}(Ux_t+Ws_{t-1})$
- $o_t = \text{softmax}(Vs_t)$
对于RNN的参数我们就是需要求U、W和V这三个矩阵,这里可以使用SGD来进行模型参数的优化,同时其梯度可以用一种叫做BPTT的当时来求得
我们使用交叉熵来定义RNN模型每一层的损失:
$$E_t(o_t,\hat{o}_t) = -o_t\log \hat{o}_t$$
则整个模型的损失通过累加可以求得:
$$E=\sum_t E_t(o_t,\hat{o}_t) = -\sum_t o_t\log \hat{o}_t$$
这里的$t$表示当前的步数(层数),$\hat{o}_t$为第$t$的预测值.
这里的梯度使用BP来计算,为了计算方便,以$t=3$为例
$$\begin{equation}\begin{split} \frac{\partial E_3}{\partial V}&= \frac{\partial E_3}{\partial \hat{o}_3} \frac{\partial \hat{o}_3}{\partial V} \\
&= \frac{\partial E_3}{\partial \hat{o}_3} \frac{\partial \hat{o}_3}{\partial z_3} \frac{\partial z_3}{\partial V} \\
&= \frac{\partial E_3}{\partial z_3} \frac{\partial z_3}{\partial V} \\
&= (\hat{o}_3-o_3)s_3 \\
\end{split}\end{equation}$$
辅助推导:
$$\begin{equation}\begin{split} \frac{\partial E}{\partial z^j}&= \frac{\partial -o\text{log}\hat{o}}{\partial z^j} \\
&= \frac{\partial -\sum_k o^k\text{log}\hat{o}^k}{\partial V^js} \\
&= -\frac{1}{s} \sum_k o^k \cdot \frac{1}{\hat{o}^k} \frac{\partial \hat{o}^k}{V_j} \\
&= \text{使用softmax推导} \\
&= -\frac{1}{s} \left( o^j \frac{1}{\hat{o}^j} s \hat{o}^j(1-\hat{o}^j) + \sum_{k:k \neq j} o^k \frac{1}{\hat{o}^k} \cdot(-s\hat{o}^j\hat{o}^k ) \right) \\
&= -\left( o^j-o^j\hat{o}^j - \sum_{k:k \neq j} o^k \hat{o}^j \right) \\
&= -\left( o^j - \hat{o}^j \sum_ko^k \right) \\
&= \hat{o}^j-o^j \\
\end{split}\end{equation}$$
其中$z_3=Vs_3$,$z^j=V^js$,$V^j$为第$j$个类别的向量权重
可以看到损失函数对$V$求梯度时最后式子是极其简单,只需要计算当前预测的$o$以及当前隐含层的$s$即可,
现在来看下对于$W$的求导,这里会有稍微的不同:
$$\frac{\partial E_3}{\partial W}=\frac{\partial E_3}{\partial \hat{o}_3} \frac{\partial \hat{o}_3}{\partial s_3} \frac{\partial s_3}{\partial W}$$
而这里$s_3$时依赖$s_2$的
$$s_3=tanh(W s_2 + Ux_3)$$
而同时$s_2$还是依赖$s_1$的,因此在对于$E_3$求$W$的导数的时候并不能将$s_2$作为一个常量进行简单的求导,这样我们再次根据链式法则将会有如下:
$$\frac{\partial E_3}{\partial W} = \sum_{k=0}^3 \frac{\partial E_3}{\partial \hat{o}_3} \frac{\partial \hat{o}_3}{\partial s_3} \frac{\partial s_3}{\partial s_k} \frac{\partial s_k}{\partial W}$$
因为这里的$W$是共享的,每一步输出都有用到,因此对于$W$的求导只需要将每一步($t=0..3$)的梯度加起来即可
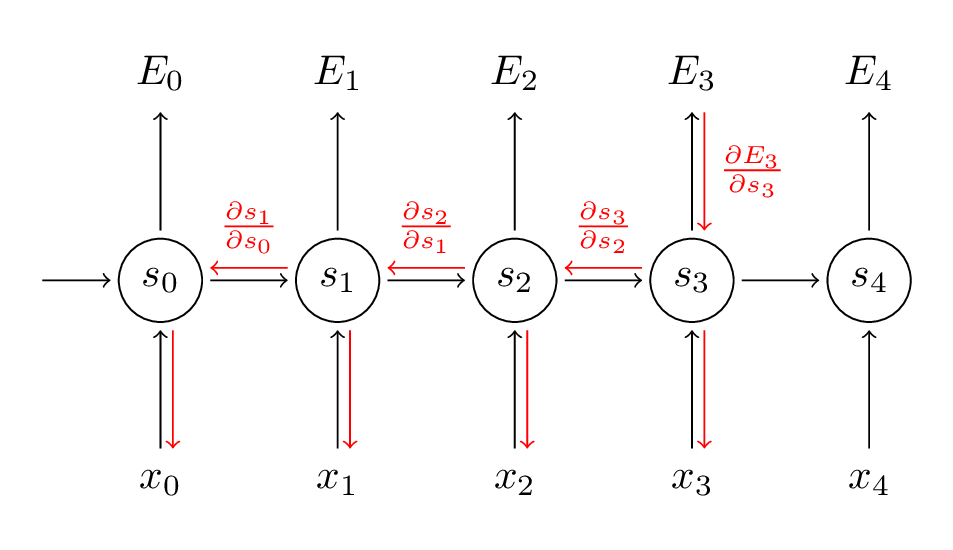
由于$U$的参与前向计算的式子也$W$的类似,因此关于$\frac{\partial E}{\partial U}$也可以用上述方式来求导。
这三个参数的梯度计算与普通的BP计算类似,最大的区别是这三个参数在每一层都是共享的。
由于在求导时需要向后计算,如果层数很多就会遇到经典的梯度消失问题,所以实际的RNN中每一个链可能都会做一个一定长度限制的截断。另外关于梯度消失的问题可以参考RNN的其他变种LSTM和GRU等.
总结
RNN与传统的神经网络最大的特别就是在每一层计算的时候可以拿到前面几层的信息,这样特别可以有效适用于序列相关的学习,当然在实际操作中效果可能没有这么好~-_-!!

