By

题目

使用递归的方法将栈颠倒

解题

假设当前的入栈顺序为1,2,3,4,5 那么我们的目标是将栈内的顺序改为5,4,3,2,1
先来看如果将数据搞成了1 和5,4,3,2 那么只需要将1放在栈的尾部即可，就可以变成了5,4,3,2,1
那么如何将2，3，4，5变为5,4,3,2呢，其实同理，也是分为2和5,4,3 一致递归

Read More

By

问题

如何将一个链表进行逆序输出，比如1->2->3->4的链表输出为4321

解题

  1. 最方便可能就是先讲原生链表翻转，再按翻转的输出，这样会破坏原有链表的结构
  2. 第二种就是先遍历存放到一个数组或者栈中，然后从后往前输出即可，就需要额外的O(n)空间。

这两种方法都是需要额外的复杂度或者空间，网络行流传更好的方法就是使用递归-_-! 神方法啊，递归一次即可。。

Read More

By

题目

将链表1->2->3->4翻转成4->3->2->1。

解题

最简单就是遍历链表，然后保存到一个数组中，然后再向后构建数组，当然，这种方式不好，会有额外开销。-_-
这里来介绍一下另一种方法：
假设现在的链表是

null->1->2->3->4->null

如果我们想办法将2移到1的前面，然后3又移到2的前面，最后将4移动3的前面，这不就完了嘛？
好，现在开始移动：

    2
   / \ 
null  1->3->4->null
将1指向2的next，然后将2的next指向head的next，然后head的next指向2

    3-2
   /  |
null  1->4->null
然后再移动3

    4-3-2
   /    |
null    1->null
再移动4

这种方式就不需要额外的空间，也只需要遍历一遍即可。

Read More

By

本文是温习快刀初试：Spark GraphX在淘宝的实践这篇文章中明风大神提到得几个graphx的应用,并且自己使用graphx将其实现一下^_^

看实验用的图：

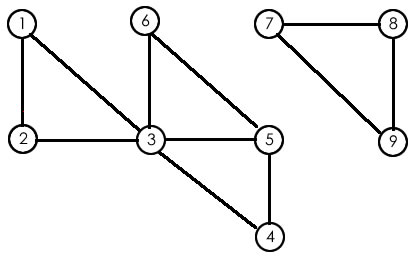
该图可以使用如下代码来进行标示

1
2
3
4
5
6
7
8
9
10
11
12
val sc=new SparkContext();
val edge=List(//边的信息
    (1,2),(1,3),(2,3),(3,4),(3,5),(3,6),
    (4,5),(5,6),(7,8),(7,9),(8,9))
   
//构建边的rdd
val edgeRdd=sc.parallelize(edge).map(x=>{
  Edge(x._1.toLong,x._2.toLong,None)
})

//构建图 顶点Int类型
val g=Graph.fromEdges(edgeRdd, 0)

Read More

By

题目

假设你有一个用 1001 个整数组成的数组,这些整数是任意排列的,但是你知道所有的整 数都在 1 到 1000(包括 1000)之间。此外,除一个数字出现两次外,其他所有数字只出现一 次。假设你只能对这个数组做一次处理,用一种算法找出重复的那个数字。如果你在运算中 使用了辅助的存储方式,那么你能找到不用这种方式的算法吗?

方法1

这里都说1~1000都至少包含一遍了，所以求和在减去1~1000的和即可
假设遍历数组之后的求和为sum，则那个数字就是sum-(1000*10001/2)

但是如果这里不是1000，而是这个数字非常的大，求和就可能出现溢出

方法2

还记得有一道经典的leetcode题目就是一个数组中每个数出现2次，只有一个数字出现了3次，找出这个数字。
该题目的思路是A^A=0,A^0=A

Read More

By

单向链表的结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Link{
	public int data;
	public Link next;
	
	public Link(int data)
	{
		this.data=data;
	}
	
	//为了打印方便而加上去的。。
	public String toString()
	{
		return String.format("data:%s",this.data);
	}
}

单向链表是否有环

这题的思路很简单，先创建两个指针都指向链表的头部，一个fast指针每次走两步，另一个slow指针每次都走一步，如果fast指针能走到null的地方就说明该单链表没有环，否则fast和slow节点一定会走到同一个节点，表示有环

Read More

By

题目

定义栈的数据结构，要求添加一个min函数，能够得到栈的最小元素。要求函数min、push以及pop的时间复杂度都是O(1)。

解题

这道题目的主要难点就是需要的复杂度为O(1)，也就是说在求最小值的时候无法遍历该栈。
正确地解法就是使用一个辅助栈（数组），为维持当前栈容量下地最小值情况

比如

栈数据
3,5,2,4,1
辅助数据
0,0,2,2,4

将5压入栈的时候，发现上一个栈顶元素下的最小值是3，故这里无法更新最小值，仍旧将当前的最小值置为3（索引位置为0），但是当2压入栈的时候
，可以发展2<3，所以在该类情况下会将当前栈的最小值更新为2（即索引为2）
这种设计在出栈的时候只需要将栈数据的栈顶出掉即可，同样在求最小值的时候只要返回当前辅助数据中索引值在栈数据中的值即可
这样就非常方便地实现了O（1）的要求，同时因为辅助栈是存储索引位置，索引并不会占用很大的内容空间

Read More

By

题目

输入一棵排序二叉树，将此树转换成一个排序的双向链表，要求不能创建任何新的借点，只能调整指针的指向.

分析

二叉排序树的中序遍历可以得到它的排序元素，但是，但是“它不能创建任何新的节点，只能调整指针的指向”，所以，直接中序法就不可行了。

大致思路是如下的：

  • 如果当前根节点的左子树不为空，则
    1. 递归左子树
    2. 查找左子树最大的元素
    3. 将该元素的right指针指向根节点，将根节点的left指针指向该元素
  • 如果当前根节点的右子树不为空，则
    1. 递归右子树
    2. 查找右子树最小的元素
    3. 将该元素的left指针指向根节点，将根节点的right指针指向该元素

Read More

By

介绍

二叉查找树（Binary Search Tree），又称二叉搜索树、二叉排序树。它符合这样的特征：

  • 它是一颗二叉树（空树也可以）
  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值
  • 它的左、右子树也也都是为二叉排序树。
      8    
    /   \
   3     10
 /   \     \
1     6     14
    /   \  /
   4    7 13

二叉查找树的搜索、插入、删除的时间复杂度等于O(h)，期望O(logn)，最坏O(n)

Read More