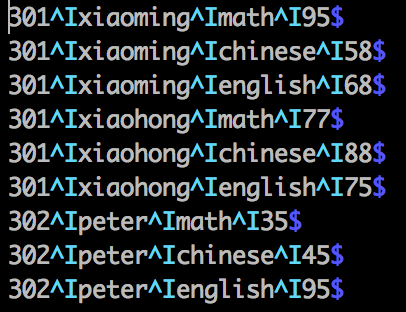
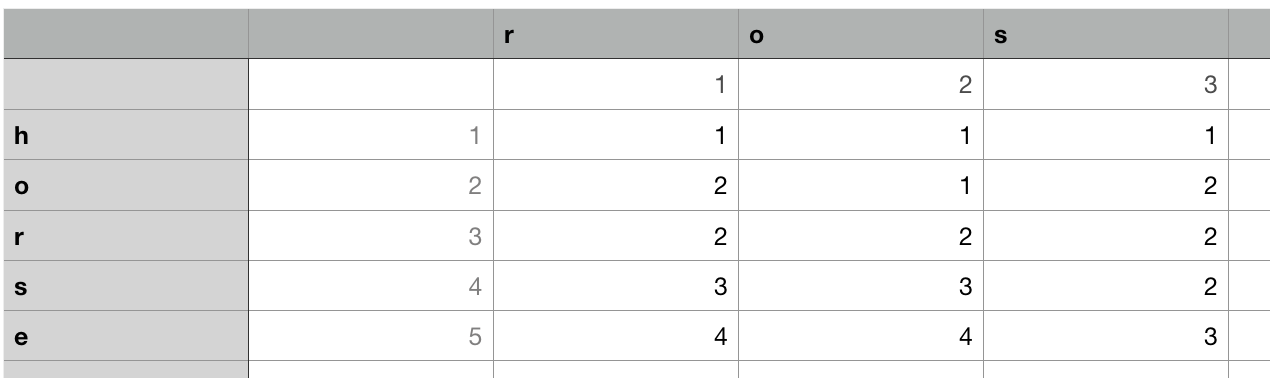
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| #include<iostream>
using namespace std;
int binary_find_k(int* A,int len1,int* B,int len2,int k){
if(len1>len2)
return binary_find_k(B,len2,A,len1,k);
if(len1 == 0)
return B[k-1];
if(k==1)
return min(A[0],B[0]);
int k1 = min(k/2,len1);
int k2 = k-k1;
cout << k1 << " , " << k2 << ":" << A[k1-1] << " , "<<B[k2-1] <<endl;
if(A[k1-1] > B[k2-1]){
cout << "keep k1" << endl;
return binary_find_k(A,len1,B+k2,len2-k2,k1);
}else if(A[k1-1] < B[k2-1]){
cout << "keep k2" << endl;
return binary_find_k(A+k1,len1-k1,B,len2,k2);
}else{
return B[k2-1];
}
}
int main(){
int A[] = {2,3,4,7,8,12};
int B[] = {1,5,6,8,10,11};
int len1 = 6;
int len2 = 7;
int k = 5;
cout << binary_find_k(A,len1,B,len2,k)<<endl;
return 0;
}
|