《台大机器学习基石》Linear Regression
Linear Regression
现在相对比于之前的Perceptron Learning Algorithm算法,假如我们现在时的问题不是解决是否发行用卡,而是该发多少额度的问题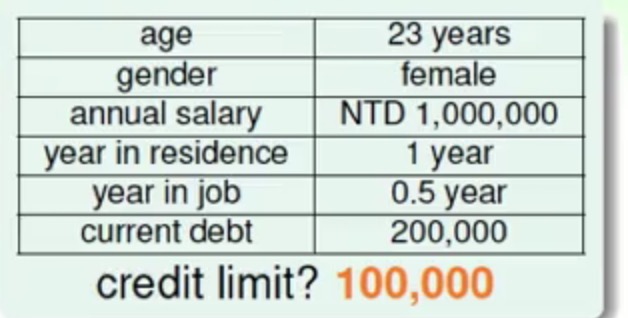
也就是输出空间属于一个实数,那么就需要一个回归算法来解决该问题!
现在相对比于之前的Perceptron Learning Algorithm算法,假如我们现在时的问题不是解决是否发行用卡,而是该发多少额度的问题
也就是输出空间属于一个实数,那么就需要一个回归算法来解决该问题!
这个总结最初是写在本地的MacDown中的,他的markdown语法解析与hexo的略微有点差异,懒得改了-_-,忍着点看..
对排版看不下去了,将本文的公式使用Latex重写了^_^ .on 2016-04-15
参考[1]
事件A和B同时发生的概率为在A发生的情况下发生B或者在B发生的情况下发生A
$$P(A \cap B) = P(A)*P(B|A) = P(B)*P(A|B)$$
所以有:
$$P(A|B)=\frac{P(B|A)*P(A)}{P(B)}$$
对于给出的待分类项,求解在此项出现的条件下各个目标类别出现的概率,哪个最大,就认为此待分类项属于哪个类别
正则化是针对过拟合而提出的,以为在求解模型最优的是一般优化最小的经验风险,现在在该经验风险上加入模型复杂度这一项(正则化项是模型参数向量的范数),并使用一个rate比率来权衡模型复杂度与以往经验风险的权重,如果模型复杂度越高,结构化的经验风险会越大,现在的目标就变为了结构经验风险的最优化,可以防止模型训练过度复杂,有效的降低过拟合的风险。
奥卡姆剃刀原理,能够很好的解释已知数据并且十分简单才是最好的模型。
我们通过上一篇文章中了解到了break point以及Growth Function之后,
我们将Growth Function的上界设为B(N,k)(maximum possible m_H(N) when break point = k),表示在break point的k的情况下,其mH(N)的最大值,用通俗的话来说,在N个点中,任意取k个点不能shatter。
这种方式定义的好处就是以后在计算不需要计较具体的成长函数是怎么样的,形成的
hypothesis究竟是如何的。
考智力,脑子不好使咋办??只有记下来^_^
烧一根不均匀的绳,从头烧到尾总共需要 1 个小时。现在有若干条材质相同的绳子,问 如何用烧绳的方法来计时一个小时十五分钟呢?
假设现在有三根绳子A和B和C,现在将A的两端都点着,B的一端都点着
半小时过去后,A就烧没了,此时B应该还有半小时的时长可以烧,但是现在把B的另一端也点着
又过了十五分钟,B也烧没了,这个时候把C的两端也都点着
又过了半小时,C也烧没了
好了,一小时十五分钟就这么烧到了^_^
其实主要思路还是两端 一端 烧得搭配
先来看一下一个经典的信用卡发放问题: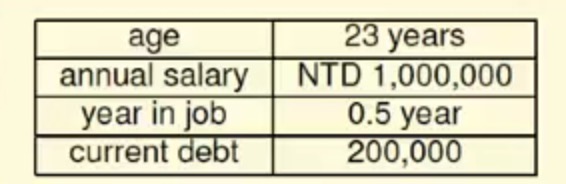
这是一个用户的基本的信息,现在要决定是否对他发放信用卡。
现在假设这些基本信息组成了一个向量X={x1,x2,…xd}
同时对于每一维度上有一个对应的权重向量W={w1,w2,…wd}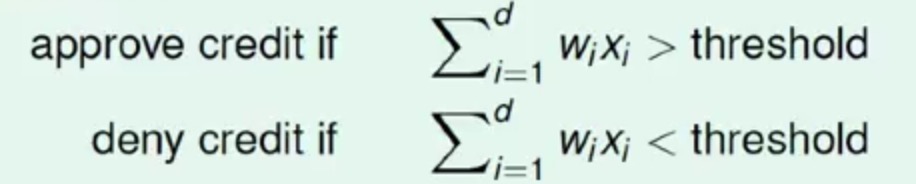
那么如果这两个向量乘积出来的值大于一个设定的阈值,我们就发他信用卡,否则就不发
输入一个整数数组,判断该数组是不是某二元查找树的后序遍历的结果。 如果是返回 true,否则返回 false。
例如输入 5、7、6、9、11、10、8,由于这一整数序列是如下树的后序遍历结果:
8
/ \
6 10
/\ /\
5 7 9 11
因此返回 true。
如果输入 7、4、6、5,没有哪棵树的后序遍历的结果是这个序列,因此返回 false
做该题之前还必须得了解什么是二叉查找树
最主要的性质就是左子树的任何节点都小于根节点,右子树的任何节点都大于根节点。
然后后序遍历的最后一位肯定是根节点,所以,可以得到巧妙的方法为:
则该序列的最后一位a[n-1]必定是根节点,然后前面的序列中连续一部分是左子树的遍历,另一部份是右子树的遍历
此时需要在前面的序列中查找第一个大于root的节点a[i]
删除指定的字符串
比如They are students 和 aeiou 则删除之后剩下Thy r stdnts
关于此类查找之类的如果能往位图上靠就是最快速的,本题也可以,一个字符是8位,也就是会出现256中情况,所以现在只需要用一个256长度的位图就可以来判断当前字符是否存在待删除的字符字典中。
一个人知道未来n天的每天股票的价格,请你给出一个算法,使得这个人从哪天买入,哪天卖出能获得最大的收益。
问题实际上就是求一个数组后面元素减前面元素的最大值
看了大神们提出了一个O(n)的方法,就是遍历过去,同时记录当前最小的那个元素,然后每次都是当前遍历元素减去最小的元素 取其差值最大